Home
Class 12
PHYSICS
To determine the half life of a radioact...

To determine the half life of a radioactive element , a student plot a graph of in `|(dN(t))/(dt)|` versus `t` , Here `|(dN(t))/(dt)|` is the rate of radioactive decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after `4.16 ` year the value of p is

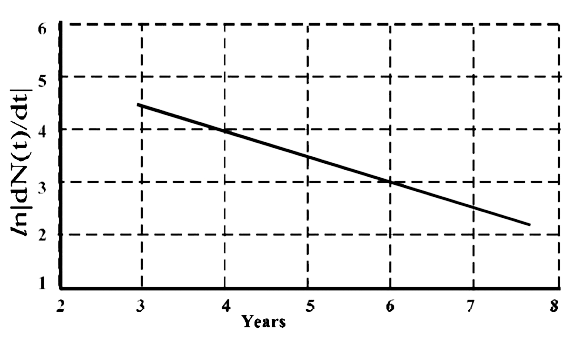
Text Solution

Verified by Experts

The correct Answer is:
8
`N =N_0 e^(-lambda t)`
`ln|dN|dt|=1n(N_0 lambda)-lambda t`
From graph
`lambda =(1)/(2)` per year
`(t_(1))/(2)=(0.693)/(1//2)=1.386` year
`4.16` years `=3t_(1//2)`
`p=8`.
Promotional Banner

Topper's Solved these Questions

  • NUCLEAR PHYSICS

    CENGAGE PHYSICS|Exercise ddp.5.1|15 Videos

  • NUCLEAR PHYSICS

    CENGAGE PHYSICS|Exercise ddp.5.2|15 Videos

  • NUCLEAR PHYSICS

    CENGAGE PHYSICS|Exercise Linked comprehension type|5 Videos

  • Moving charges and magnetism

    CENGAGE PHYSICS|Exercise Question Bank|20 Videos

  • NUCLEI

    CENGAGE PHYSICS|Exercise QUESTION BANK|59 Videos

Similar Questions

Explore conceptually related problems

To determine the half life of a radioactive element , a student plot a graph of in |(dN(t))/(dt)| versus t , Here |(dN(t))/(dt)| is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16 year the value of p is

The half life of a radioactive element is T and its initial activity at t=0 is A_(0) and at t=t it is A, then

The half life of a radioactive substance is T_(0) . At t=0 ,the number of active nuclei are N_(0) . Select the correct alternative.

The half life of a radioactive element is 8 hours. A given number of nuclei of that element is reduced to 1//4 of that number after two hours.

If T is the half-life of a radioactive material, then the fraction that would remain after a time (T)/(2) is

The t_(0.5) of a radioactive element is related to its average life by the expression

The graph between number of decayed atoms N' of a radioactive element and time t is.