A proton (charge `1.6xx10^(-19) C, mass = 1.67xx10^(-27) kg)` is shot with a speed `8xx10^6 ms^-1` at an angle of `30^@` with the X-axis. A uniform magnetic field `B=0.30 T` exists along the X-axis. Show that path of the proton is a helix. Find the radius and pitch of the helix.

Explanation

The situation is shown in

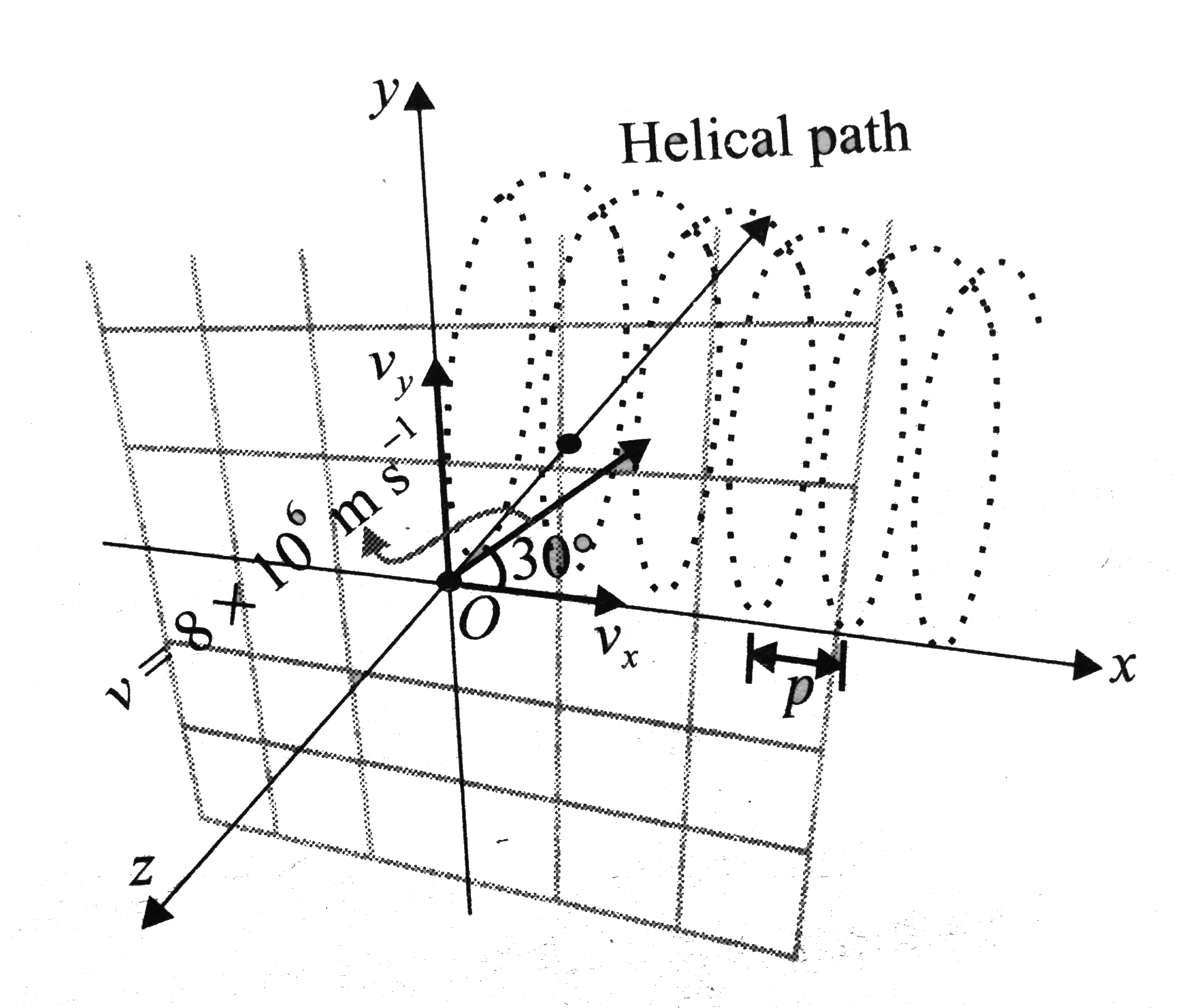
`v_x=v cos30^@=(8xx10^6)(0.866)=6.93xx10^6ms^-1`
`v_y=v sin30^@=(8xx10^6)(0.5)=4.0xx10^6ms^-1`
Since the velocity has both components, parallel and transverse to magnetic field, so the resulting path will be helix. Due to combined action of `v_x, v_y` and B, the proton moves in a helical path. The radius of helix is
`r=(mv_y)/(qB) =((1.67^10^-27)(4xx10^6))/((1.6xx10^-19)xx0.3)=0.139m`
Time taken to complete one circle:
`T=(2pim)/(qB)=(2pi1.6xx10^-27)/(1.6xx10^-19xx0.3)=2.16xx10^-7s`
The pitch of the helix
=distance travelled by the proton along x-axis in time T.
`=v_xxxT=(6.93xx10^6)xx(2.19xx10^-7)=1.515m`