The magnetic field is confirmed in a square region. A positive charged particle of charge q and mass m the limiting velocities of the particles so that it may come out of face (1), (2), (3), and (4).

Explanation

For the positive charge coming out from face (1), the radius of the path in magnetic field should be less than or equal to `l//4`, For limiting case
`r_(max)=l/4=(mv)/(qB) implies v_(max)=(qBl)/(4m)`

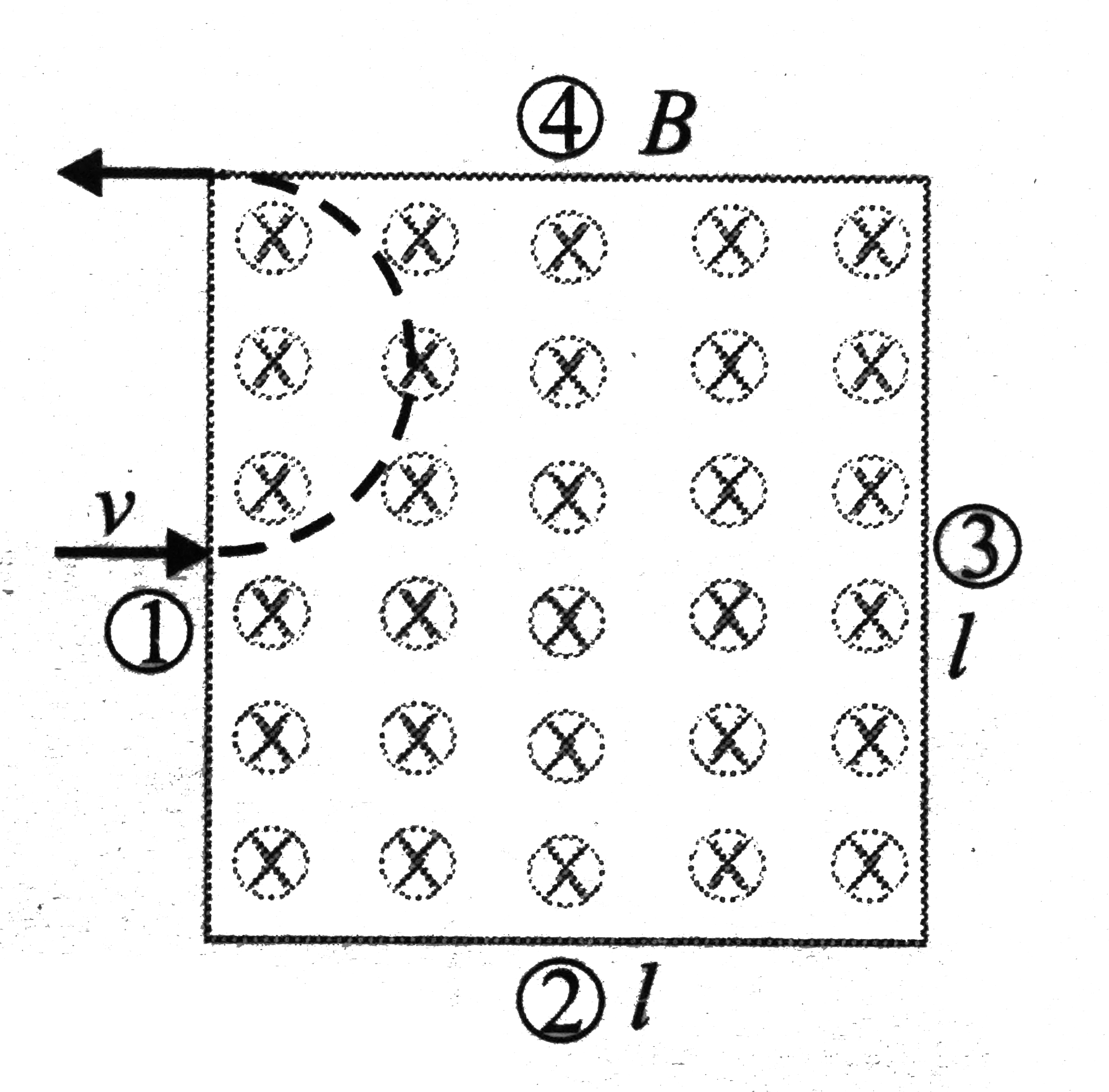
Hence, if the velocity is `lt(qBl)/(4m)`, the charge particle comes out of face (1).
We can observe for right palm rule that the particle cannot come out from face(1).
For a positive charge comming out of face (4), let particle come out at pont N from
`DeltaOMN`
`(OM^2)=(ON^2)+(MN^2)`
`r^2=(r-1.2)^2+l^2 impliesr=5/4l`

If the particle comes out from face (4), `rlt5/4limplies (mv)/(qB) lt5/4l`
or `vlt5/4(qBl)/m`. If velocity `vgt5/4(qBl)/m`, the particle will come out from face(3).