Home
Class 12
PHYSICS
A charge particle of mass m and charge q...

A charge particle of mass m and charge q is projected with velocity v along y-axis at `t=0.`

Find the velocity vector and position vector of the particle `vec v (t) and vec r (t)` in relation with time.

Text Solution

Verified by Experts

Radius of the circular path `R=(mv)/(qB)`
Angular velocity of the particle `omega=v/R=(qB)/m`
The speed of the particle will remain unchanged. The centre of circular path will be located on z-axis at point C. Let us take time interval t. during this time interval the particle will rotate an angel `theta=omegat=(qBt)/m`.
Let us draw the front view of the circular path and locate the instantaneous position of the particle.

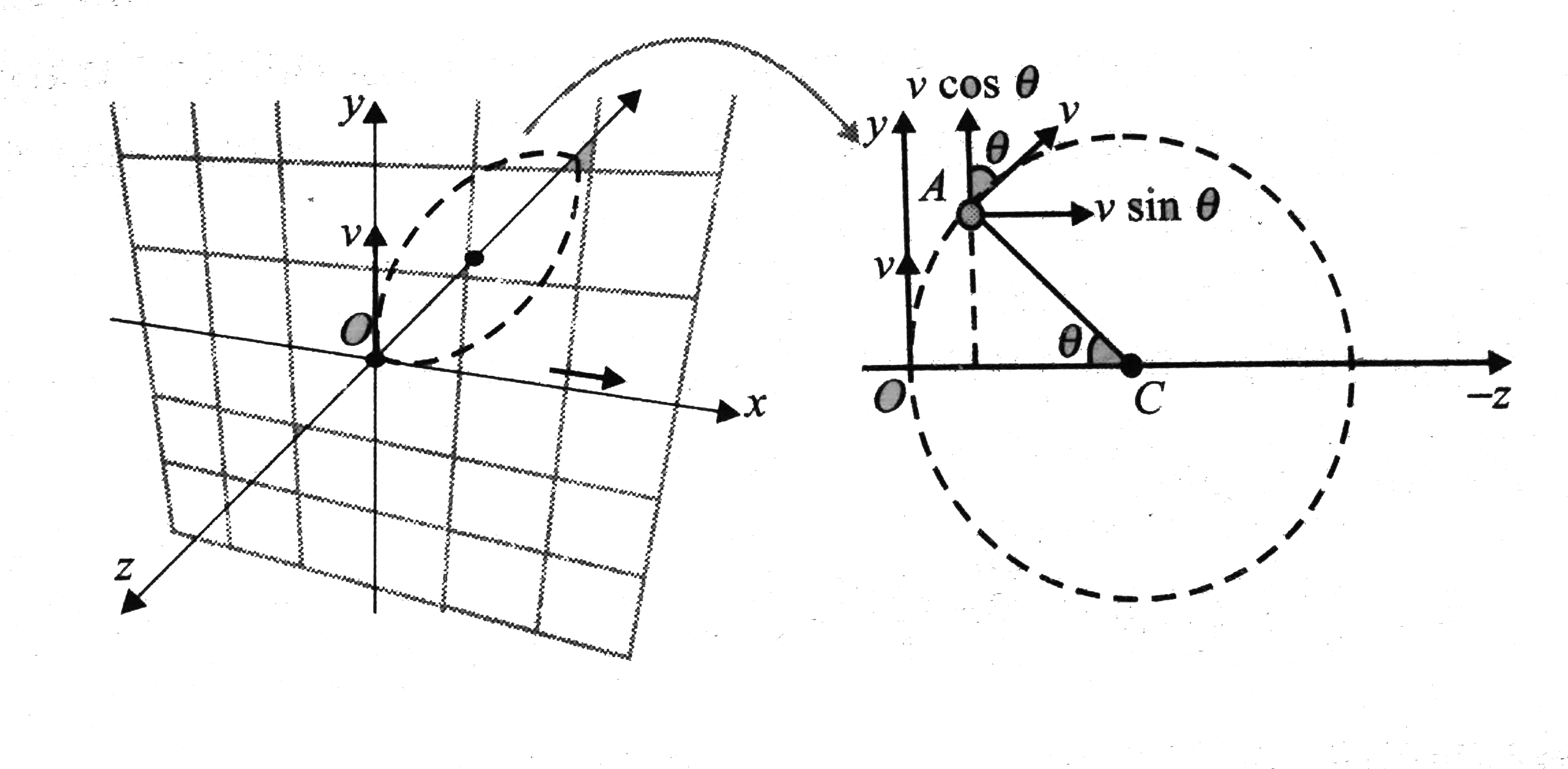
Writing velocity vector at time t.
`vecv=v cos theta hatj-v sin theta hatk`
`vecv(t)=vcos ((qBt)/(m))hatj-v sin ((qBt)/(m))hatk`
Now writing y and z coordinates of the particle.
y-coordinate of `P=R sin theta`
z-coordinate of `P=-(R-R cos theta)`
`vecr(t)=r sin.(qBt)/(m) j-R(1-cos.(qBt)/(m))hatk`
[where `R=(mv)/(qB)`].
Promotional Banner

Topper's Solved these Questions

  • MAGNETIC FIELD AND MAGNETIC FORCES

    CENGAGE PHYSICS|Exercise Solved Example|25 Videos

  • MAGNETIC FIELD AND MAGNETIC FORCES

    CENGAGE PHYSICS|Exercise Exercise 1.1|22 Videos

  • KINETIC THEORY

    CENGAGE PHYSICS|Exercise Question Bank|31 Videos

  • Magnetism and Matter

    CENGAGE PHYSICS|Exercise Question Bank|50 Videos

Similar Questions

Explore conceptually related problems

In a right handed coordinate system XY plane is horizontal and Z-axis is vertically npward. A uniform magnetic field exist in space in vertically npward direction with magnetic induction B. A particle with mass m and charge q is projected from the origin of the coordinate system at t= 0 with a velocity vector given as vec(v) = v_(1) hat(i) + v_(2) hat(k) Find the velocity vector of the particle after time t.

A particle of mass m and charge q is projected into a uniform magnetic field underset(B)to=-B_(0)hatK with velocity underset(V)to-V_(0)hati from origin. The position vector of the particle at time t is underset(r)to . Find the impulse of magnetic force on the particle by the time underset(r)to.underset(V)to becomes zero for the first time.

A particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time t=(pim)/(2qB) .

The velocity vector of the motion described by the position vector of a particle, r = 2t hati + t^(2) hatj is given by

If in previous illustration, The charge particle is projected at angle alpha with x-axis with magnitude of velocity. Find a. velocity vector in function of time vec v (t). b. position vector in function of time vec r (t).

A particle of mass m and charge q travelling at a velocity v along x -axis at time t=0 . It enters a region in which electric field, E is present along z -axis and magnetic field, B is present along y -axis. The distance covered upto time t=0.2xx10^(-1) sec, along x -axis is v//50 (in meters). find the value of v :

A particle of mass m is travelling with a constant velocity v=v_(0)hati along the line y=b,z=0 . Let dA be the area swept out by the position vector from origin to the particle in time dt and L the magnitude of angular momentum of particle about origin at any time t. Then

There exist uniform magnetic and electric fields of manitudes 1T and 1Vm^-1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms^-1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time pis will be

A particle of specific charge alpha is projected from origin with velocity v=v_0hati-v_0hatk in a uniform magnetic field B=-B_0hatk . Find time dependence of velocity and position of the particle.