Consider a nonconducting plate of radius r and mass m which has a charge q distributed uniformly over it. The ring is rotated about its axis with an angular speed `omega` Show that the magnetic moment `mu` and the angular momentum I of the plate are rlated as `mu = (q)/(2m)l.`

Explanation

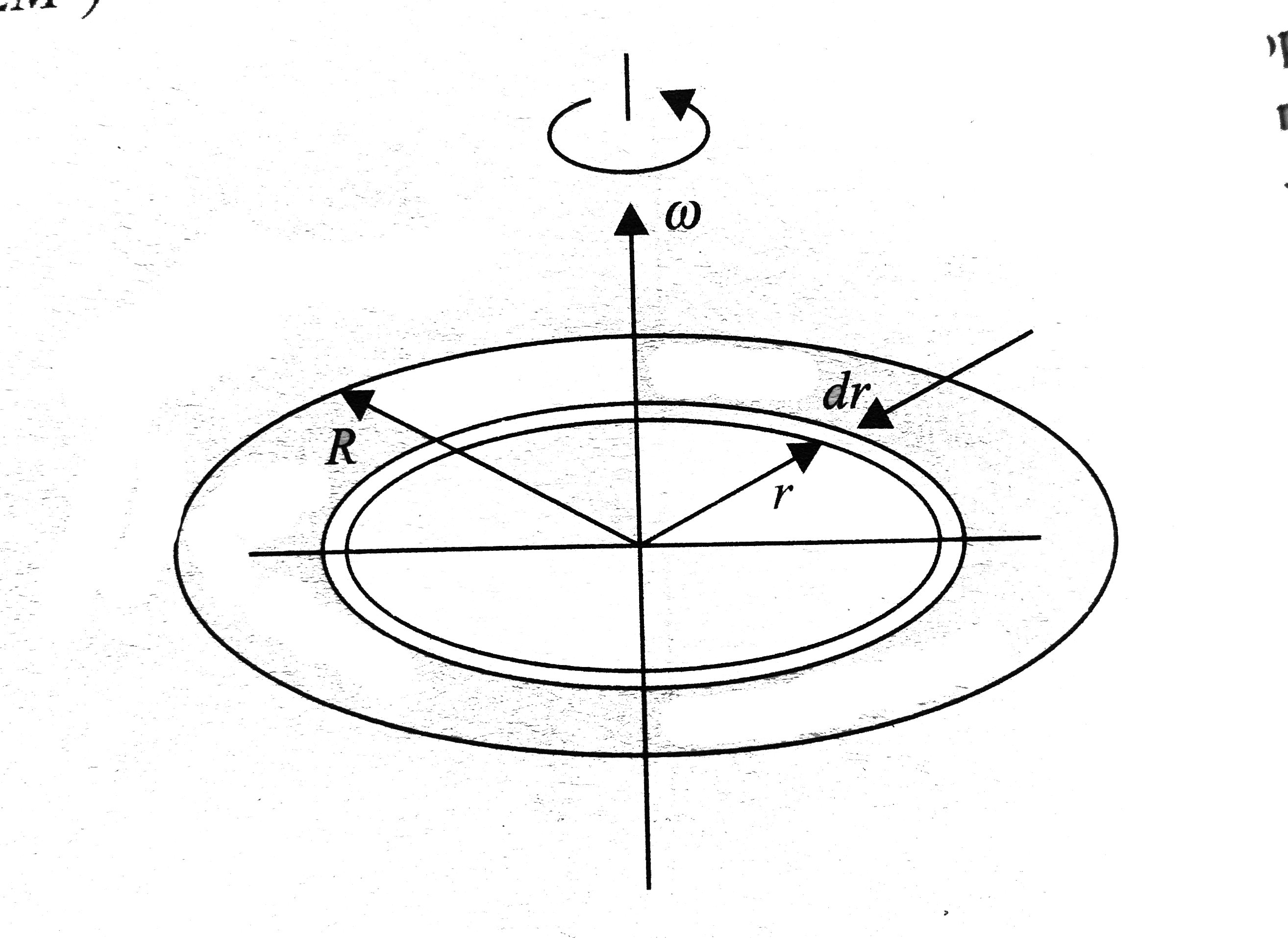
The charge is distributed on the surface of the disk.
We consider a differential ring of radius r and thickness dr.
The charge on the element is `dq=sigmadA=sigma(2pirdr)`
The magnetic moment of the ring `dmu=(dI)A=(dI)pir^2`
The current in the differential ring
`dI=(dq)f=(sigmadA) omega/(2pi)=(sigma^2omegardr)=sigmaomegardr`
The magnetic moment of the differential ring,
`dmu(sigmaomegardr)pir^2=pisigmaomegar^3dr`
`mu=intdmu=int_0^Rpisigmaomegar^3dr=1/4pisigmaomegaR^4`
The magnetic vector `vecmu` is parallel to `vecomega` if charge is
positive.
`vecmu=1/4pisigmaR^4vecomega`
In terms of total charge `Q=sigmapiR^2`, the magnetic moment is
`vecmu=1/4QR^2vecomega`
The angular momentum of disk is `veL=(1/2MR^2)vecomega` and
`vecmu=(Q/(2M))vecL`.

This is a general result for any rigid body of any arbitrary shape
having mass M and charge Q.