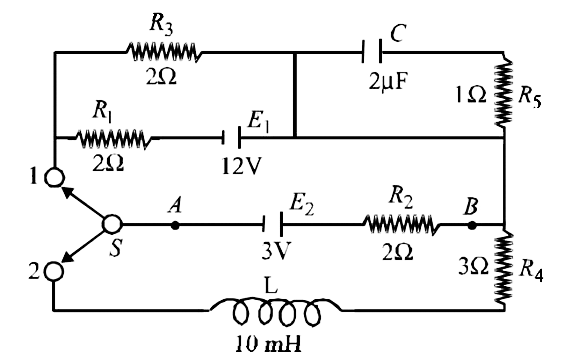
a. The capacitor offers infinite resistance to dc in the steady state, therefore, the current in capacitor branch is zero. The equivalent circuit, in steady state, when switch is in position (1) is given in Fig.
The distribution of current according to kirchhoff's first law is shows in Fig. Applying kirchhoff's second law to mesh abcda,
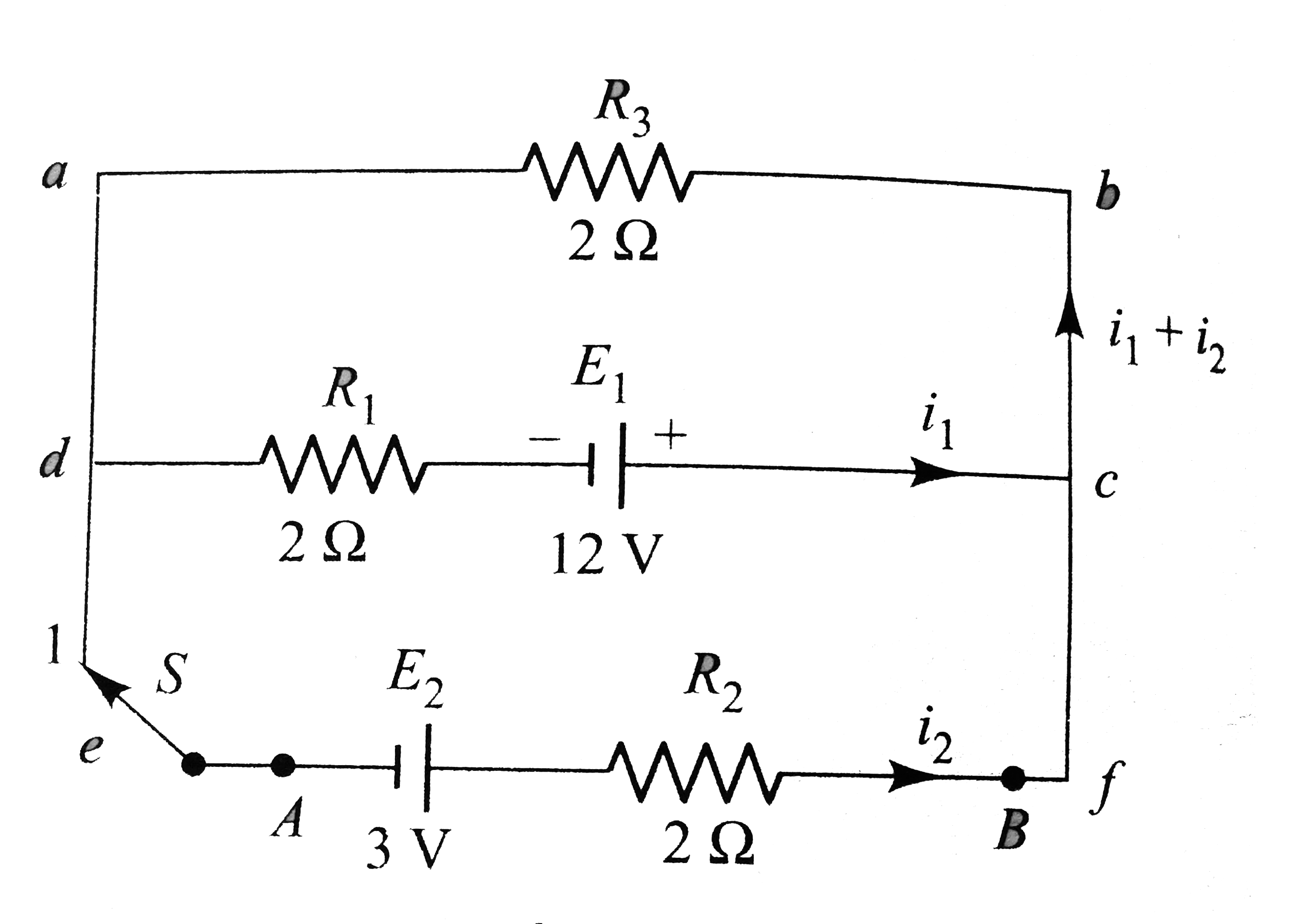
`i_(1) xx 2 + (i_(1) + i_(2)) xx 2 = 12`
or `4i_(1) + 2i_(2) = 12` or `2i_(1) + i_(2) = 6` (i)
Applying kirchhoff's second law to mesh abfea,
`i_(2) xx 2 + (i_(1) + i_(2)) 2 = 3` or `2i_(1) + 4i_(2) = 3` (ii)
Solving Eqs (i) and (ii), we get `i_(1) = 3.5 A, i_(2) =- 1A`
`:.` Potential difference between `A` and `B` is
`V_(B) - V_(A) = V = E_(2) - i_(2)R_(2) = 3 - (- 1) xx 2 = 5 V`
`:. V_(A) - V_(B) = - 5V`
b. When switch `S` is put in position 2, the equivalent circuit takes the form as shows in Fig.
Total resistance of the circuit,
`R = R_(2) + R_(4) = 2 + 3 = 5 Omega`
`L = 10 mH = 10 xx 10^(-3) H`
In steady state, there is not role of inductor `L`.
`:.` Steady current
`i_(0) = (E)/(R) = (3)/(5) = 0.6 A`

The growth of current in `RL` circuit is given by
`i = i_(0) (1-e^(-(R)/(L)t))` i.e., `(i)/(i_(0)) = (1-e^(-(R)/(L)t))`
Given `i = (i_(0))/(2)`, i.e., `(i)/(i_(0)) = (1)/(2)` after time `t`.
`:. (1)/(2) = 1 - e^((R)/(L)t)` or `e^((R)/(L)t) = (1)/(2)`
i.e., `(R)/(L) t = log_(e)2`
i.e., `t = (L)/(R) log_(e) 2 = (10 xx 10^(-3))/(5) log_(e) 2 = 1.38 xx 10^(-3) s`
The current at the instant, `i = i_(0)//2 = 0.3 A`
`:.` Energy stored,
`U = (1)/(2) Li^(2) = (1)/(2) xx 10 xx 10^(-3) xx (0.3)^(2) = 4.5 xx 10^(-4) J`