A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
INDUCTANCE
CENGAGE PHYSICS|Exercise Archives (integer)|2 VideosINDUCTANCE
CENGAGE PHYSICS|Exercise Subective Type|2 VideosINDUCTANCE
CENGAGE PHYSICS|Exercise Archives (multiple Correct)|3 VideosHEATING EFFECT OF CURRENT
CENGAGE PHYSICS|Exercise Thermal Power in Resistance Connected in Circuit|28 VideosKINETIC THEORY
CENGAGE PHYSICS|Exercise Question Bank|31 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-INDUCTANCE-Archives (linked Compreshension)
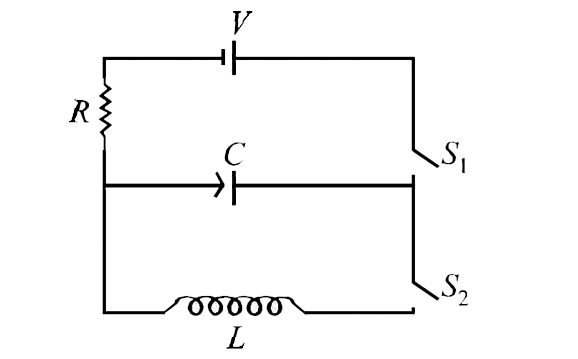
- In the given circuit the capacitor (C) may be charged through resistan...
Text Solution
|
- In the given circuit the capacitor (C) may be charged through resistan...
Text Solution
|
- In the given circuit the capacitor (C) may be charged through resistan...
Text Solution
|
- Modern train are based on maglev technology in which trains are magnti...
Text Solution
|
- Modern train are based on maglev technology in which trains are magnti...
Text Solution
|
- Modern train are based on maglev technology in which trains are magnti...
Text Solution
|
- A point charges Q is moving in a circular orbit of radius R in the x-y...
Text Solution
|
- A point charges Q is moving in a circular orbit of radius R in the x-y...
Text Solution
|