A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Multiple Correct|35 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Assertion Reasoning|6 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Subjective|21 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Single Correct
- A particle is performing SHM. Its kinetic energy K varies with time t ...
Text Solution
|
- Two particle P and Q describe S.H.M. of same amplitude a same frequenc...
Text Solution
|
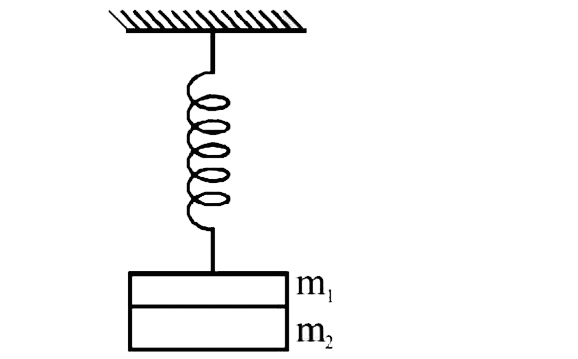
- Two masses (m1) and (m2) are suspended together by a massless spring o...
Text Solution
|
- A body of mass m is released from a height h to a scale pan hung from ...
Text Solution
|
- Frequency of a particle executing SHM is 10 Hz. The particle is suspen...
Text Solution
|
- The potential energy of a particle of mass 1kg in motion along the x- ...
Text Solution
|
- An object of mass 0.2 kg executes simple harmonic oscillation along th...
Text Solution
|
- The string of a simple pendulum replaced by a uniform rod of length L ...
Text Solution
|
- A uniform semicurcular ring having mass m and radius r is hanging at o...
Text Solution
|
- Two springs with negligible masses and force constants k1=200(N)/(m) a...
Text Solution
|
- A thin uniform vertical rod of mass m and length l pivoted at point O ...
Text Solution
|
- A particle executes SHM with time period 8 s. Initially, it is at its ...
Text Solution
|
- A particle executed S.H.M. starting from its mean position at t=0, If ...
Text Solution
|
- In a certain oscillatory system (particle is performing SHM), the ampl...
Text Solution
|
- A particle of mass m moving along x-axis has a potential energy U(x)=a...
Text Solution
|
- The instantaneous displacement x of a particle executing simple harmon...
Text Solution
|
- A simple harmonic motion along the x-axis has the following properties...
Text Solution
|
- A spring balance has a scale that can read from 0 to 50 kg. The length...
Text Solution
|
- A soil cylinder of mass M and radius R is connected to a spring as sho...
Text Solution
|
- A block A is connected to spring and performs simple harmonic motion w...
Text Solution
|
 .
.