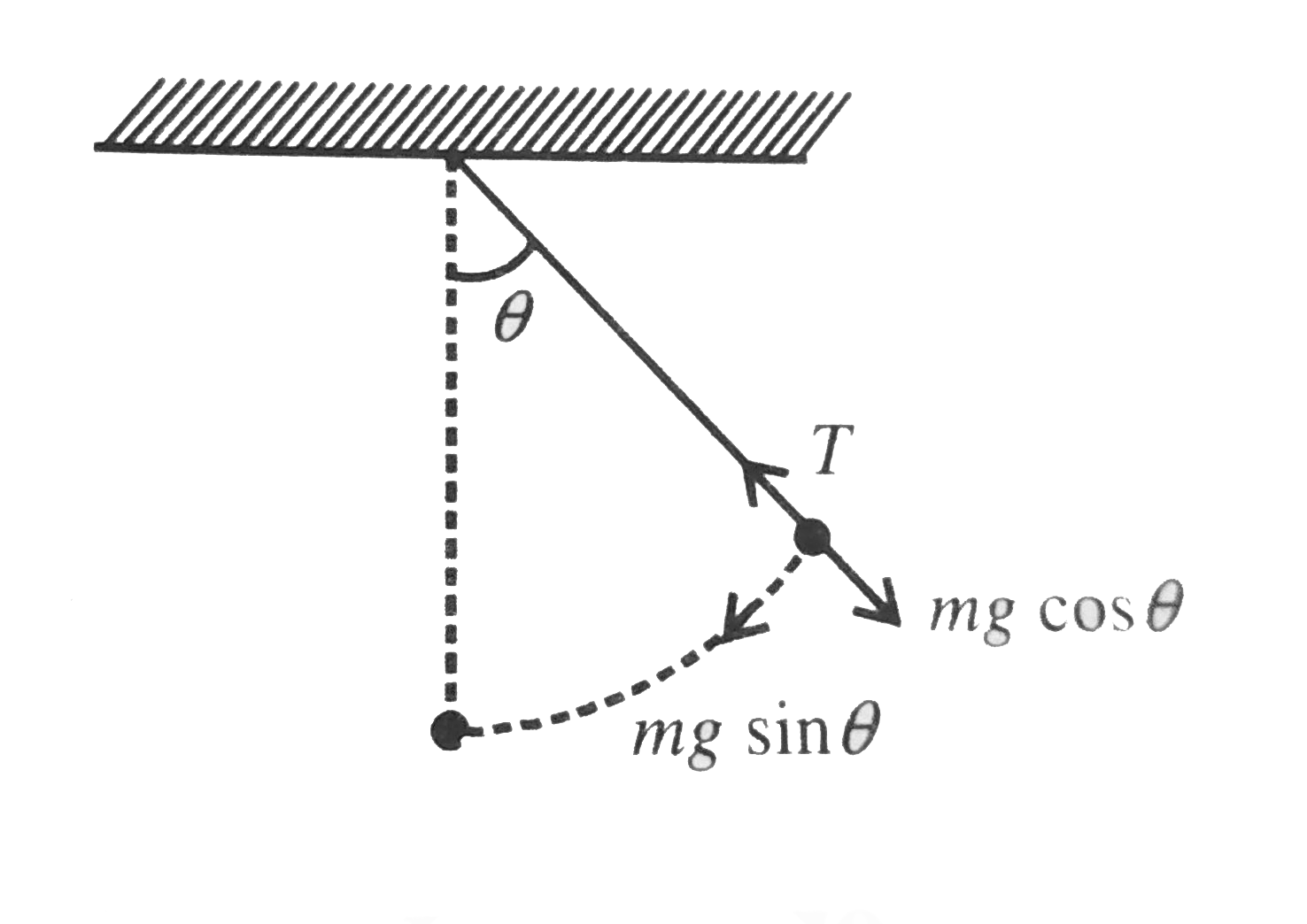
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Comprehension|33 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Integer|10 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Multiple Correct|35 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Assertion Reasoning
- Q. Statement I: The total energy of a particle performing simple harmo...
Text Solution
|
- Q. Statement I: Two cubical blocks of same material and of sides a and...
Text Solution
|
- Q. Statement I Three pendulums are suspended from ceiling as shown in ...
Text Solution
|
- A. Statement I is true statement II is true, Statement II is a correct...
Text Solution
|
- STATEMENT-1 : In simple pendulum performing S.H.M., net acceleration i...
Text Solution
|
- Statement I: If the amplitude of a simple harmonic oscillator is doub...
Text Solution
|