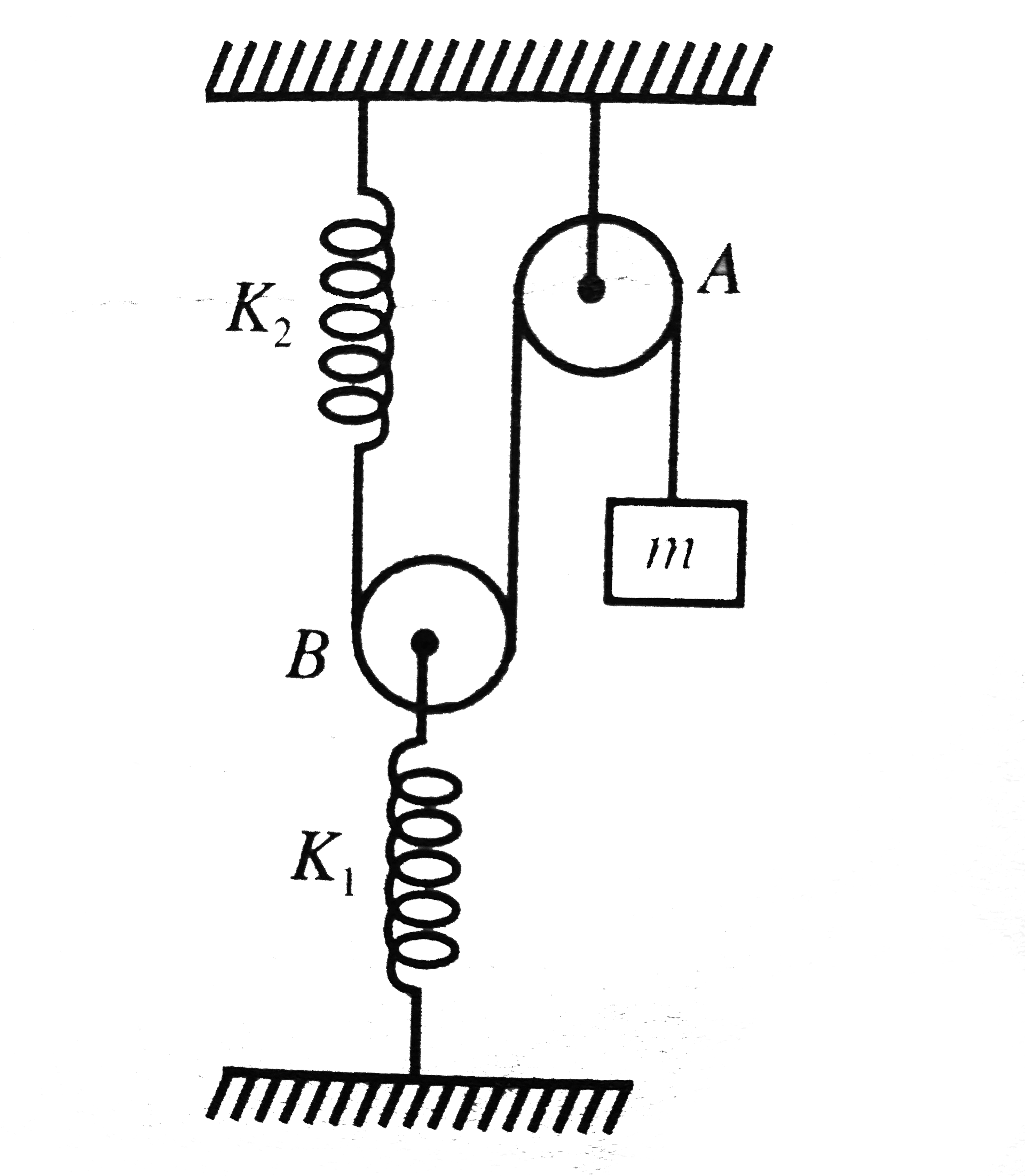
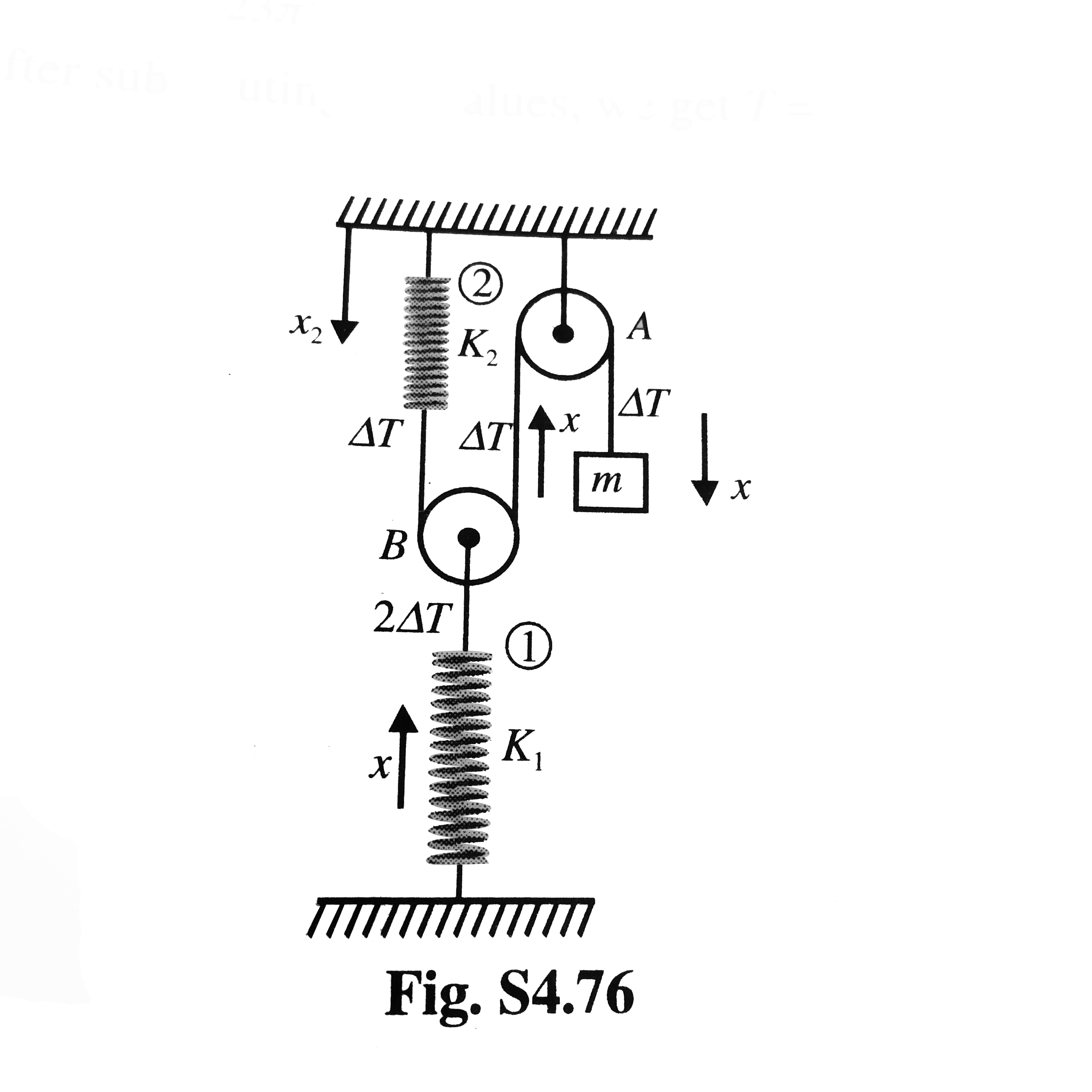
Text Solution
Verified by Experts
Topper's Solved these Questions
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Subjective type|2 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Multiple Correct Answer Type|6 VideosLINEAR AND ANGULAR SIMPLE HARMONIC MOTION
CENGAGE PHYSICS|Exercise Comprehension|33 VideosKINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
CENGAGE PHYSICS|Exercise Interger|11 VideosMISCELLANEOUS KINEMATICS
CENGAGE PHYSICS|Exercise Interger type|3 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-LINEAR AND ANGULAR SIMPLE HARMONIC MOTION-Integer
- Two uniform ropes having linear mass densities m and 4m are joined to ...
Text Solution
|
- In the figure shown, mass 2m connected with a spring of force constant...
Text Solution
|
- Two simple pendulums A and B having lengths l and (l)/(4) respectively...
Text Solution
|
- A weightless rigid rod with a small iron bob at the end is hinged at p...
Text Solution
|
- A rod of mass m and length l hinged at one end is connected by two spr...
Text Solution
|
- A block of mass m is tied to one end of a spring which passes over a s...
Text Solution
|
- A uniform disc of mass m and radius R is pivoted smoothly at its centr...
Text Solution
|
- A uniform disc of mass m and radius R=(80)/(23pi^2)m is pivoted smooth...
Text Solution
|
- In the arrangement shown if Fig. Pulleys are small and light and sprin...
Text Solution
|
- A small body of mass m is connected to two horizontal spring of elasti...
Text Solution
|