A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-ARCHIVES 2 VOLUME 6-Comprehension
- Waves y(1) = Acos(0.5pix - 100pit) and y(2)=Acos(0.46pix - 92pit) are ...
Text Solution
|
- Waves y(1) = Acos(0.5pix - 100pit) and y(2)=Acos(0.46pix - 92pit) are ...
Text Solution
|
- Waves y(1) = Acos(0.5pix - 100pit) and y(2)=Acos(0.46pix - 92pit) are ...
Text Solution
|
- Two trains A and B moving with speeds 20m//s and 30m//s respectively i...
Text Solution
|
- Two trains A and B moving with speeds 20m//s and 30m//s respectively i...
Text Solution
|
- Two trains A and B moving with speeds 20m//s and 30m//s respectively i...
Text Solution
|
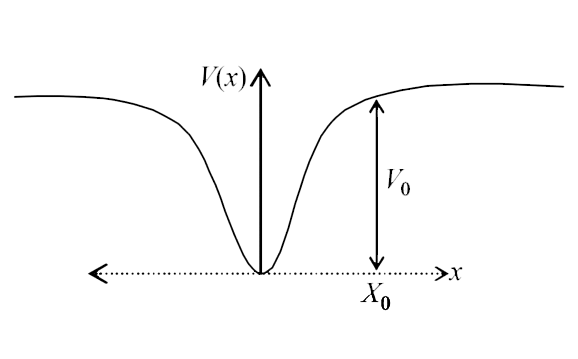
- When a particle of mass m moves on the x-axis in a potential of the fo...
Text Solution
|
- When a particle of mass m moves on the x-axis in a potential of the fo...
Text Solution
|
- When a particle of mass m moves on the x-axis in a potential of the fo...
Text Solution
|
- Phase space deagrams are useful tools . in analyzing all kinds of dy...
Text Solution
|
- Phase space deagrams are useful tools . in analyzing all kinds of dy...
Text Solution
|
- Phase space deagrams are useful tools . in analyzing all kinds of dy...
Text Solution
|
 .
.