A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ROTATIONAL DYNAMICS
A2Z|Exercise Work And Energy In Case Of Rotation|22 VideosROTATIONAL DYNAMICS
A2Z|Exercise Rotation And Translation Combined And Rolling Motion|18 VideosROTATIONAL DYNAMICS
A2Z|Exercise Torque , Torque Equation And Equilibrium Of A Rigid Body|29 VideosPROPERTIES OF MATTER
A2Z|Exercise Chapter Test|29 VideosTHERMAL PROPERTIES OF MATTER
A2Z|Exercise Chapter Test|30 Videos
Similar Questions
Explore conceptually related problems
A2Z-ROTATIONAL DYNAMICS-Angular Momentum And Its Conservation
- A particle mass 1 kg is moving along a straight line y=x+4. Both x and...
Text Solution
|
- A circular platform is mounted on a vertical frictionless axle. Its ra...
Text Solution
|
- An solid cylinder of mass 20 kg and radius 20 cm rotates about its axi...
Text Solution
|
- A child is standing with his two arms outstretched at the centre of a ...
Text Solution
|
- Two discs of moments of inertia I1 and I2 about their respective axes,...
Text Solution
|
- A ballet dancer, dancing on a smooth floor is spinning about a vertica...
Text Solution
|
- A man stands on a rotating platform with his arms stretched holding a ...
Text Solution
|
- A uniform solid disk of mass m = 3.0 kg and radius r = 0.20 m rotates ...
Text Solution
|
- A projectile of mass m is launched with an initial velocity vec vi mak...
Text Solution
|
- In previous problem, the angular momentum of the projectile about the ...
Text Solution
|
- A conical pendulum consists of a bob of mass m in motion in a circular...
Text Solution
|
- A uniform solid sphere of radius r = 0.500 m and mass m = 15.0 kg turn...
Text Solution
|
- A disk with moment of inertia I1 rotates about frictionless, vertical ...
Text Solution
|
- A playground merry-go-round of radius R = 2.00 has a moment of inertia...
Text Solution
|
- A 60.0-kg woman stands at the western rim of a horizontal turntable ha...
Text Solution
|
- A student sits on a freely rotating stool holding dumbbells, each of m...
Text Solution
|
- A puck of mass m = 50.0 g is attached to a taut cord passing through a...
Text Solution
|
- A horizontal platform in the shape of a circular disk rotates on a fri...
Text Solution
|
- A bar of mass 'm' length 'l' is in pure translatory motion with its ce...
Text Solution
|
- A girl of mass M stands on the rim of a frictionless merry-go-round of...
Text Solution
|
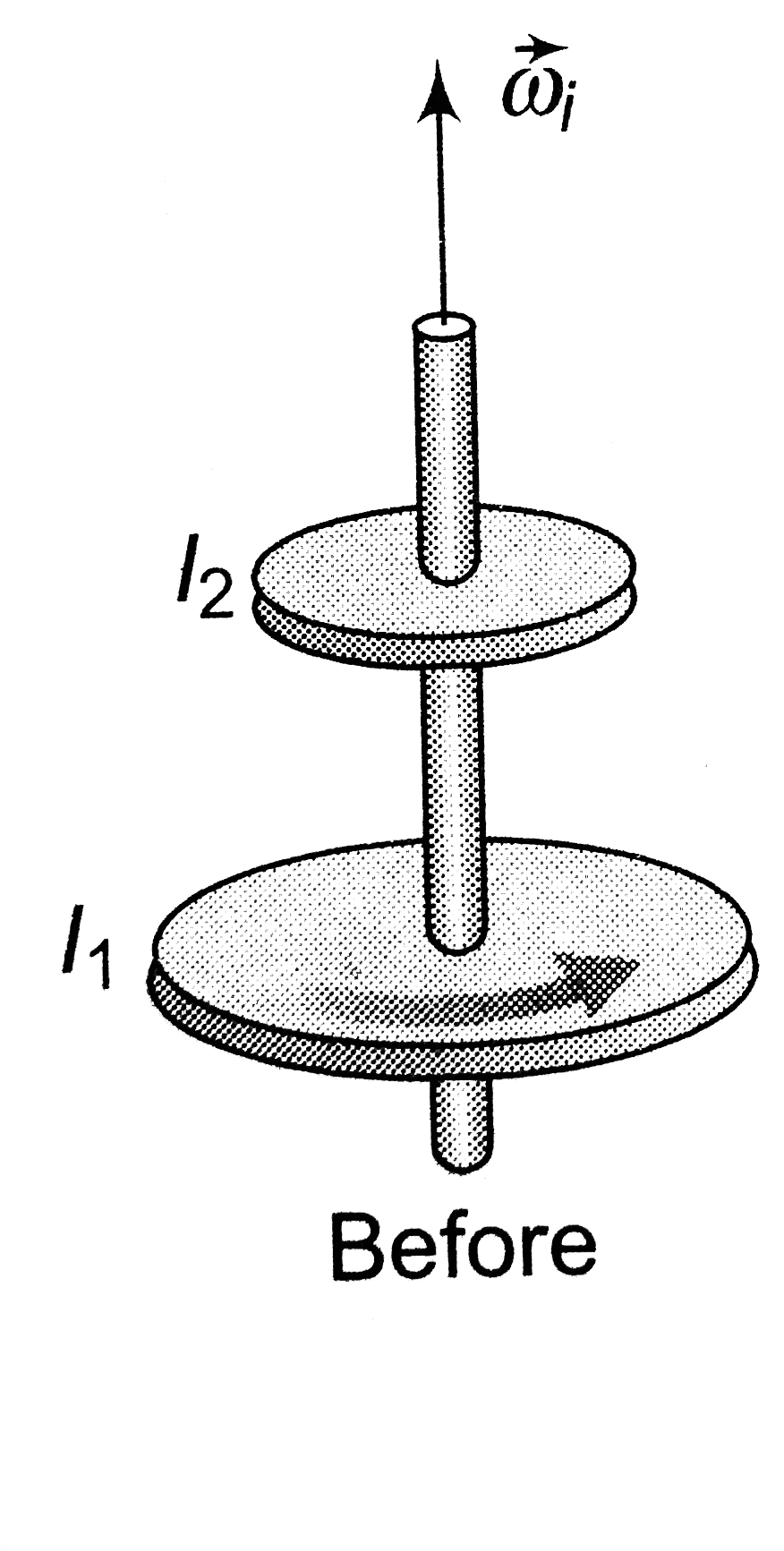 .
.