Text Solution
Verified by Experts
Topper's Solved these Questions
KINEMATICS
PRADEEP|Exercise 4 Conceptual Problems|1 VideosKINEMATICS
PRADEEP|Exercise 4 Con ceptual Problems|22 VideosKINEMATICS
PRADEEP|Exercise 2 Con ceptual Problems|15 VideosGRAVIATION
PRADEEP|Exercise Assertion-Reason Type Questions|19 VideosLAWS OF MOTION
PRADEEP|Exercise Assertion- Reason Type Questions|17 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-KINEMATICS-3 Con ceptual Problems
- Two vectors vec(a) and vec(b) are such that |vec(a)+vec(b)|=|vec(a)-ve...
Text Solution
|
- The three vectors vec A, vec B and vec C are repesented in magnitude a...
Text Solution
|
- Show that the displacement vector does not depend upon the choece of t...
Text Solution
|
- ABCD is a parallelogram Fig. 2 (c ) .64. AC and (BD) are its diagonals...
Text Solution
|
- The greatest resultant of two vectors vec P and vec Q is (n) times the...
Text Solution
|
- ABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of ...
Text Solution
|
- Can a rectangular component of a vector be greater than the vector its...
Text Solution
|
- Can a flight of a bird be an example of composition of vectors ?
Text Solution
|
- A room has dimensions 3 m xx 4 m xx5 m. A fly starting at one cronet e...
Text Solution
|
- A vecto vec A has magnitude 2 and another vector vec B has magnitude 3...
Text Solution
|
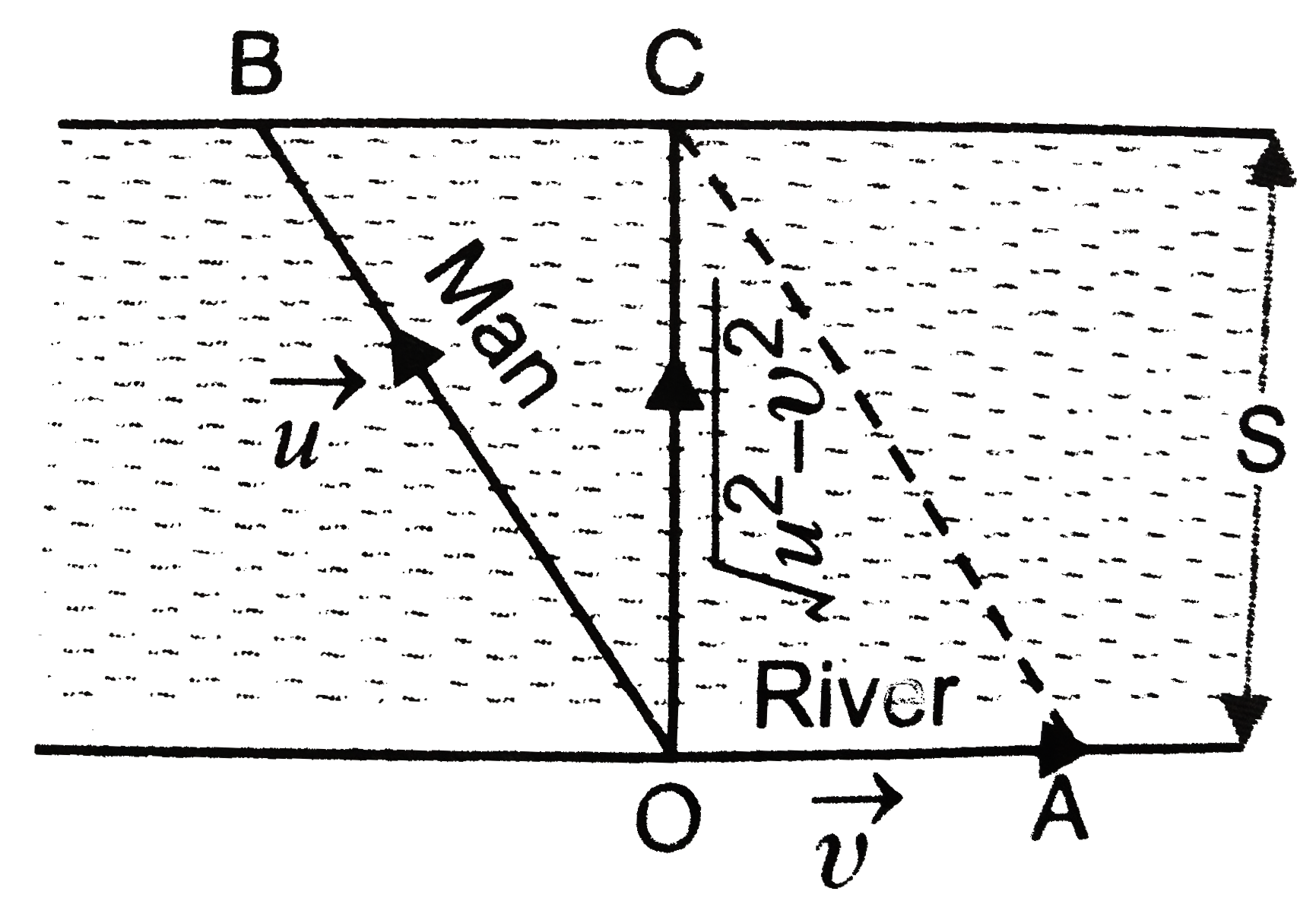
- A man directly crosses a river in time t1 and swims down the current a...
Text Solution
|
- An aeroplane takes off at an angle or 30^(@) to the horizontal. If the...
Text Solution
|
- A plane is travlling eastward at a speed of 400 km h^)-1) . Wind is b...
Text Solution
|
- A weight mg is suspended from the middle of a rope whose ends are at t...
Text Solution
|
- If vec A. vec B = vec A. vec C, is it correct to conclude that vec B ...
Text Solution
|
- Three vector vec(A),vec(B), vec(C ) satisfy the relation vec(A)*vec(B)...
Text Solution
|
- If vec A xx vec B=vec A xx vec C, is it correct to conclude that vec B...
Text Solution
|
- If vec A xx vec B= vec C xx vec B, show that vec C need not be equal t...
Text Solution
|
- If three vectors vec A, vec B and vec C are such that vec A .vec B =...
Text Solution
|
- In an Delta ABC as showin in Fig. 2 . (2) .71 (a) prove that a/(sin...
Text Solution
|
 .
.