Home
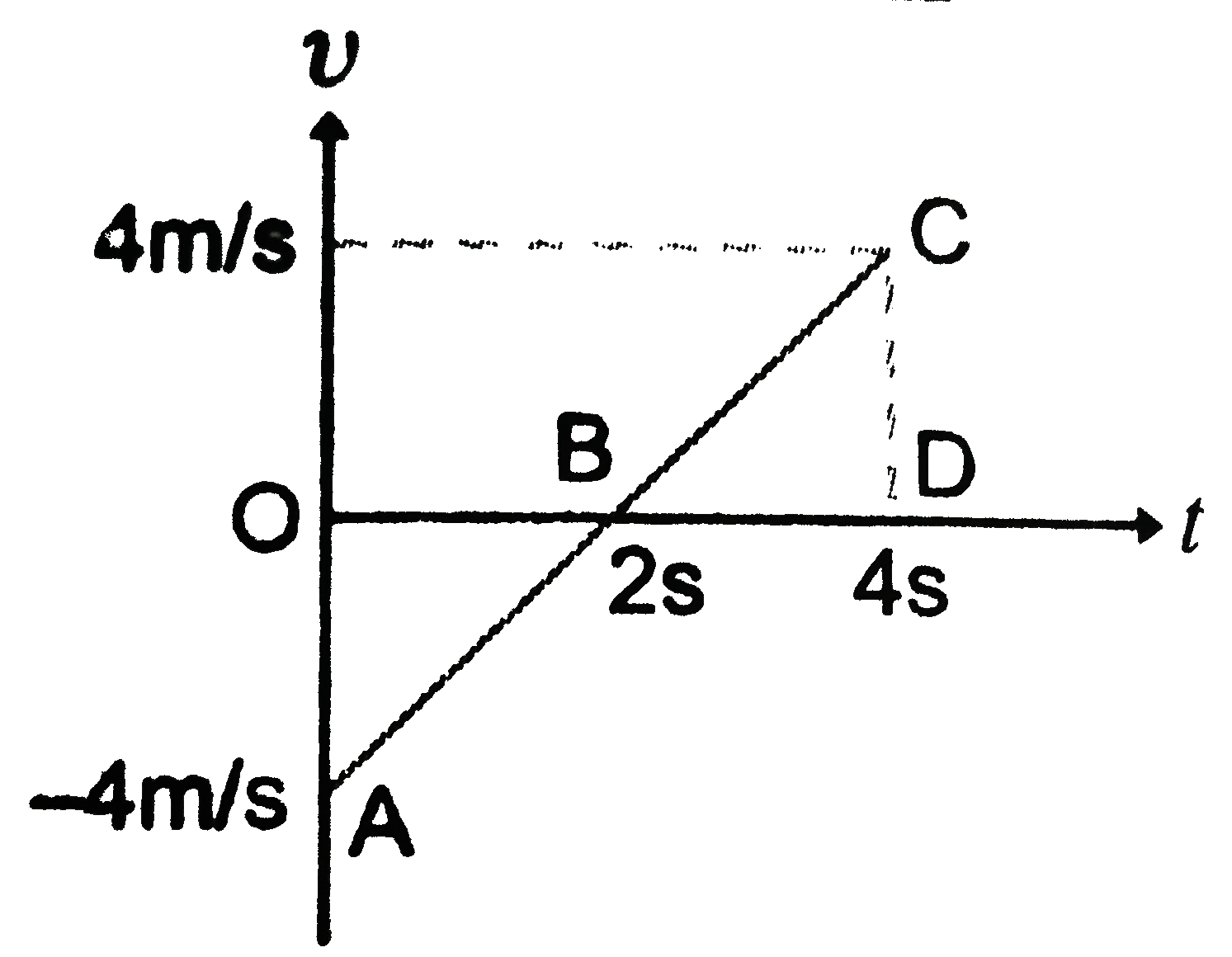
Class 11
PHYSICS
The displacement of a particle is moving...

The displacement of a particle is moving by `x = (t - 2)^2` where `x` is in metres and `t` in second. The distance covered by the particle in first `4` seconds is.

A

` 4 m`

B

` 8 m`

C

` 12 m`

D

` 16 m`

Text Solution

Verified by Experts

The correct Answer is:
A
Here, ` x = (t - 2) ^2 , velcity , ` v = 9dx0/(dt) = 2 ( t-2) m//s , acceleration, ` a= (dv) /(dt0 =2 ms^(-2)` (i.e. uniform)`
When ` t=0 , v =- m//s , t = 2 s , v-0`
` t= 4 s, v = 4 m//s`.
Velocity 9v) -time (t) graph of this motion is as shown in Fig. 2 (EP) , 4 `
Distance travelled = area ` AOB = ( 4 xx2 )/2 + ( 4 xx 2)/2 = 8m`
.
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    PRADEEP|Exercise 2 NCERT multiple|15 Videos

  • KINEMATICS

    PRADEEP|Exercise 3 NCERT multiple|161 Videos

  • KINEMATICS

    PRADEEP|Exercise 4 Fill in the blanks|11 Videos

  • GRAVIATION

    PRADEEP|Exercise Assertion-Reason Type Questions|19 Videos

  • LAWS OF MOTION

    PRADEEP|Exercise Assertion- Reason Type Questions|17 Videos

Similar Questions

Explore conceptually related problems

The displacement of a partcle is given by x=(t-2)^(2) where x is in metre and t in second. The distance coverred by the particle in first 3 seconds is

The position x of a particle varies with time t as x = 6 + 12t - 2 t^2 where x is in metre and in seconds. The distance travelled by the particle in first five seconds is

The x -coordinate of a particle moving along x -axis varies with time as x=6-4t+t^(2), where x in meter and t in second then distance covered by the particle in first 3 seconds is

The displacement of a particle moving in a straight line is described by the relation s=6+12t-2t^(2) . Here s is in metre and t in second. The distance covered by the particle in first 5s is

The displacement of a particle moving in a straight line, is given by s = 2t^2 + 2t + 4 where s is in metres and t in seconds. The acceleration of the particle is.

x - t equation of a particle in SHM is x = (4 cm)cos ((pi)/(2)t) Here , t is in seconds. Find the distance travelled by the particle in first three seconds.

The displacement of a particle is represented by the equation, s=3 t^3 =7 t^2 +4 t+8 where (s) is in metres and (t) in seconds . The acceleration of the particle at t=1 s is.

The displacement of a particle is given by y=(6t^2+3t+4)m , where t is in seconds. Calculate the instantaneous speed of the particle.

Force acting on a particle is given by F=(A-x)/(Bt) , where x is in metre and t is in seconds. The dimensions of B is -