Text Solution
Verified by Experts
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise VALUE BASED QUESTIONS|5 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise CURIOSITY QUESTIONS|4 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise ADDITIONAL EXERCISES|11 VideosRAY OPTICS
PRADEEP|Exercise Problem For Practice(a)|25 VideosTHERMODYNAMICS
PRADEEP|Exercise Assertion- Reason Type Questions|19 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-QUESTIONS
- Two forces 50N and 100 N are acting on a rod capable of rotating it ab...
Text Solution
|
- A small object of uniform density rolls up a curved surface with an in...
Text Solution
|
- A circular plate of unifrom thickness has a diameter of 56 cm. A circu...
Text Solution
|
- A stone of mass m tied to the end of a string is whirled around in a h...
Text Solution
|
- A threaded rod with 12 turns//cm and diameter 1.18 cm is mounted horiz...
Text Solution
|
- Find the centre of mass of a unifrom disc of radius a from which a cir...
Text Solution
|
- A solid cylinder of mass 20 kg and radius 0.12 m rotating wit initial ...
Text Solution
|
- Point masses m(1) and m(2) are placed at the opposite ends of a rigid ...
Text Solution
|
- A ball of mass 10^(-2) kg and having charge + 3 xx 10^(-6)C is tied at...
Text Solution
|
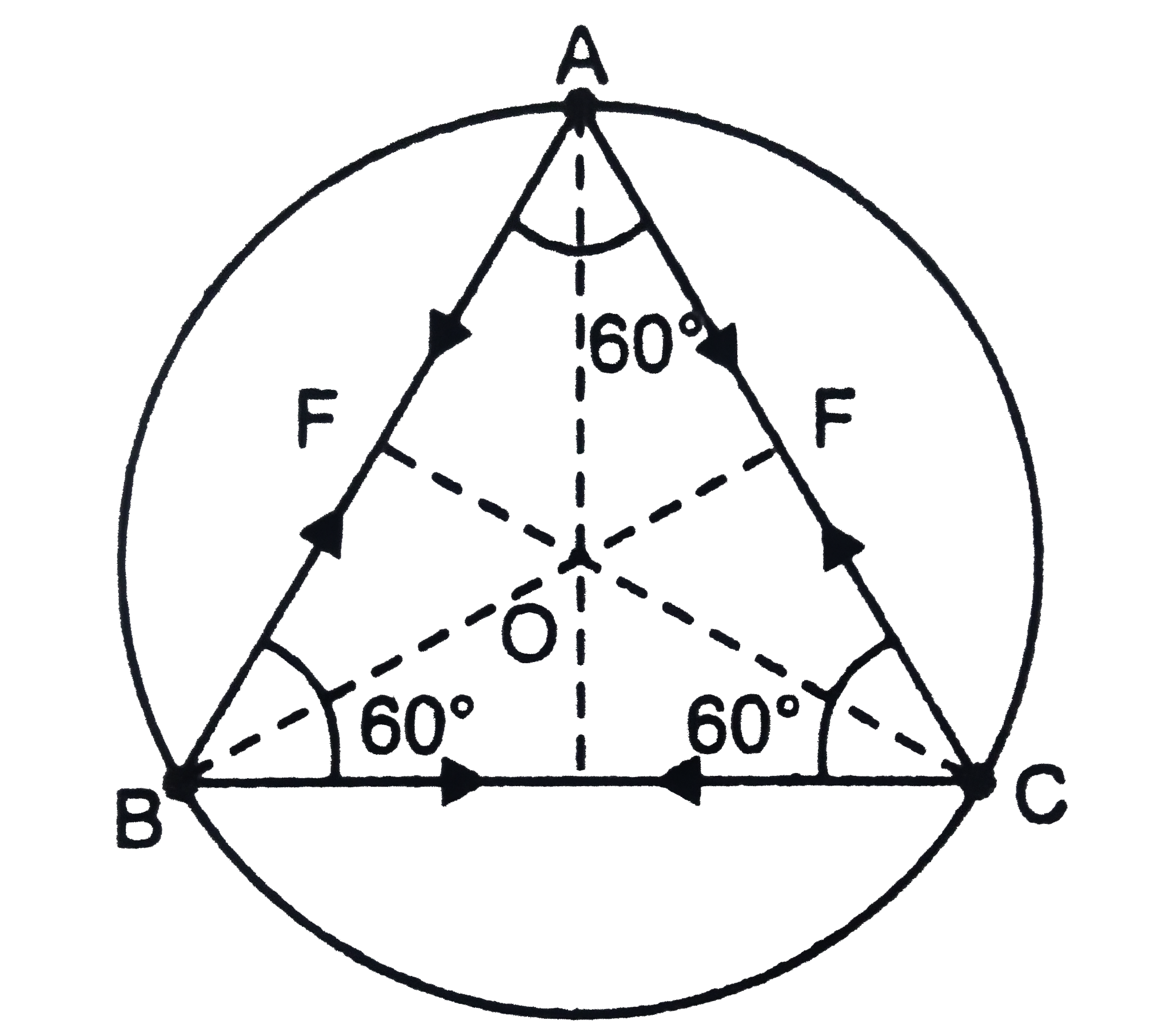
- Three particles, each of the mass m are situated at the vertices of an...
Text Solution
|
- From a uniform circular disc of diameter d,a circular disc of diameter...
Text Solution
|
- A spot light S rotates in a horizontal plane with a constant angular v...
Text Solution
|
- A nail is located at a certain distance vertically below the point of ...
Text Solution
|
- A uniform sphere of mass m and radius R is placed on a rough horizonta...
Text Solution
|
- A carpet of mass M is rolled along its length so as to from a cylinder...
Text Solution
|