The unit cell of `CsCl` has cubic arrangement of `Cl^(-)` ions and `Cs^(+)` ion is present in the body centre of the cube. Therefore, the unit cell contains one `Cs^(+)` and one `Cl^(-)` ion, `i.e.,z=1`
Molar mass of `CsCl=168.5g mol^(-1)`
Now Density`rho=(zxxm)/(a^(3)xxN_(0))`
or `a^(3)=(1xx168.5)/(3.99xx6.023xx10^(23))`
`=7.02xx10^(-23)cm^(3)`
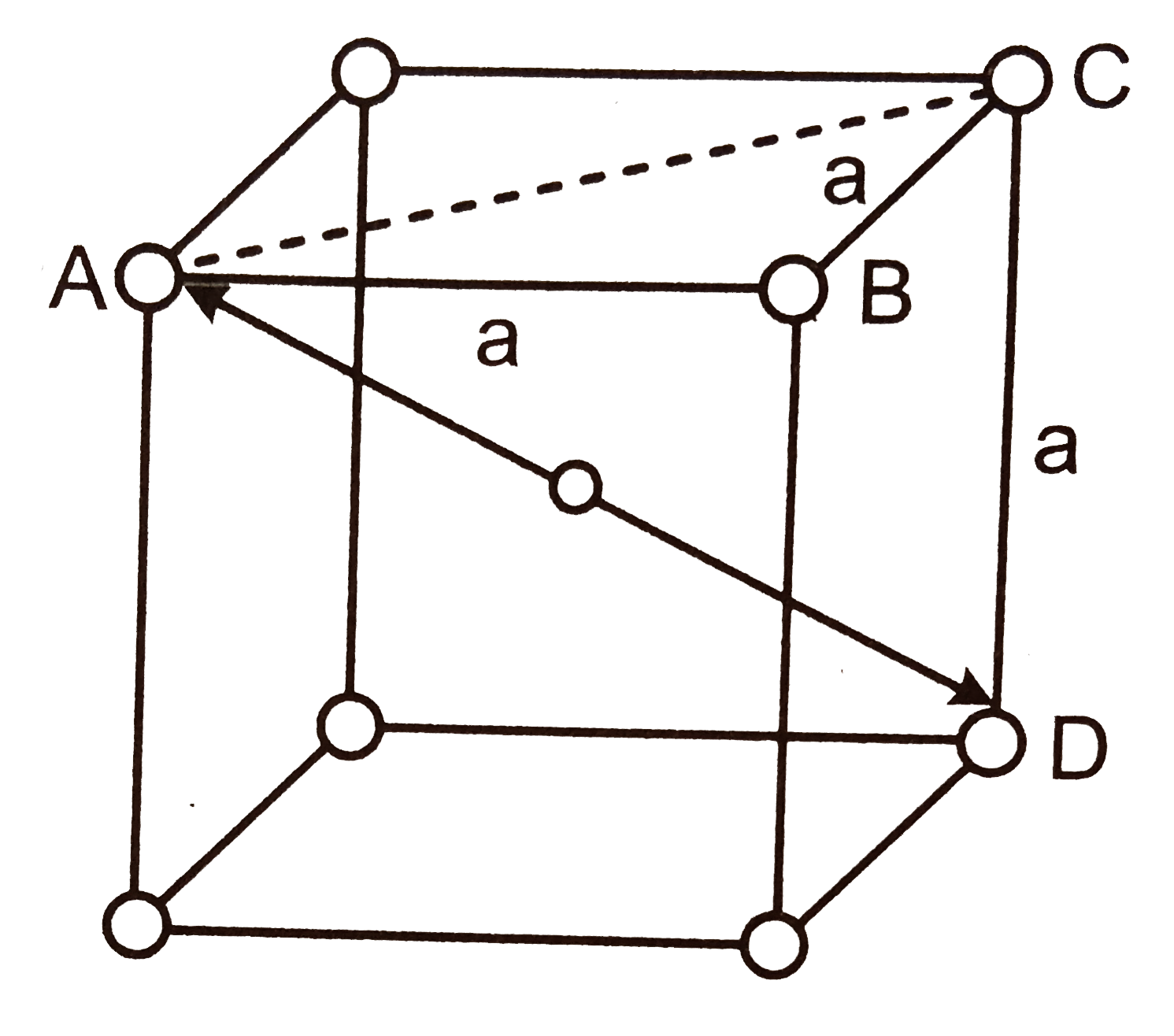
As shown in figure, `Cs^(+)` ion is present in the centre of unit cell and is in contact with `8 Cl^(-)` ion at the corners. It is clear that the length of the body diagonal is equal to twice the distance between centre of `Cs^(+)` and centre of `Cl^(-)` ion. The body diagonal can also be calculated as `:`
If the length of unit cell edge is `a`, then face diagonal `AC` is `:`
`AC=sqrt(AB^(2)+BC^(2))=sqrt(a^(2)+a^(2))=sqrt(2).a`
The body diagonal `AD=sqrt(AC^(2)+CD^(2))`
`=sqrt(2a^(2)+a^(2))=sqrt(3).a`
Now, `2(` distance between `Cs^(+)` and `Cl^(-))=sqrt(3).a`
or Distance between `Cs^(+)` and `Cl^(-)=(sqrt(3))/(2).a`
`=(sqrt(3))/(2)xx412=356.8p m`