लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
NAVBODH-तरंग प्रकाशिकी -दीर्घ उत्तरीय प्रश्न
- पोलेरॉइड क्या हैं ? इसकी बनावट , कार्य - विधि एंव उपयोग लिखिए ।
Text Solution
|
- पोलेरॉइड क्या हैं ? समतल ध्रुवित प्रकाश पोलेरॉइड से कैसे प्राप्त करेंग...
Text Solution
|
- प्रकाश के व्यतिकरण के व्दि - स्लिट प्रयोग में प्रकाश की अधिकतम तथा न्य...
Text Solution
|
- दो तरंगों के व्यतिकरण के लिए सैध्दांतिक रुप से संपोषी एंव विनाशी व्यति...
Text Solution
|
- प्रकाश के व्यतिकरण से आप क्या समझते हैं ? दो तरंगे जिनके आयाम a(1) "व"...
Text Solution
|
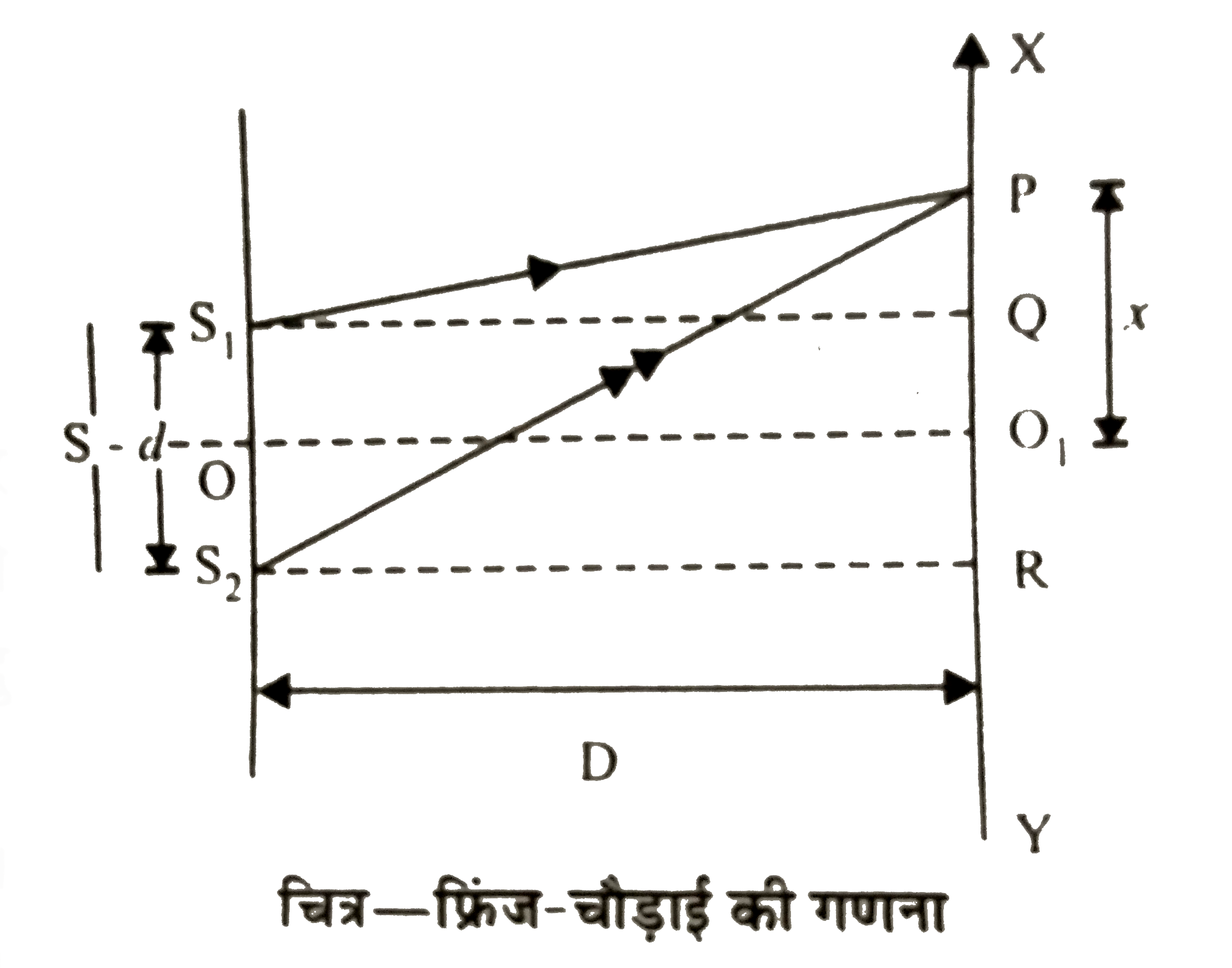
- यंग के द्विस्लिट प्रयोग में फ्रिंज चौड़ाई के लिए व्यंजक व्युत्पन्न की...
Text Solution
|
- मेलस का नियम लिखिए।
Text Solution
|
- हाइगेंस का सिद्धांत लिखिए। इस सिद्धांत का उपयोग करते हुए रेखाचित्र खीं...
Text Solution
|
- हाइगेंस सिद्धांत को लिखिए। द्वितीयक तरंगिकाओं की ज्यामितीय रचना का उपय...
Text Solution
|
- हाइगेंस सिद्धांत को लिखिए। द्वितीयक तरंगिकाओं की ज्यामितीय रचना का उपय...
Text Solution
|
- यंग के द्विस्लिट प्रयोग में पर्दे के किसी बिंदु पर (i) संपोषी और (ii) ...
Text Solution
|
- यंग के द्विस्लिट प्रयोग में प्रेक्षित व्यतिकरण प्रतिरूप और एकल स्लिट व...
Text Solution
|
- प्रकाश का विवर्तन क्या है ? एकल स्लिट विवर्तन प्रयोग में कोण के साथ ती...
Text Solution
|
- हाइगेंस का सिद्धांत लिखिए। इस सिद्धांत का उपयोग करते हुए व्याख्या कीजि...
Text Solution
|
- दिखाइए कि प्रथम विवर्तन फ्रिंज की कोणीय चौड़ाई केंद्रीय उच्चिष्ठ की को...
Text Solution
|
- यदि एकवर्णी प्रकाश स्रोत को श्वेत प्रकाश से प्रतिस्थापित कर दिया जाए त...
Text Solution
|
- चित्र खींचकर समझाइए कि किस प्रकार एक पोलेरॉइड अध्रुवित प्रकाश को ध्रुव...
Text Solution
|
- अध्रुवित प्रकाश का एक पुँज काँच-वायु के अंतरापृष्ठ पर आपतित होता है । ...
Text Solution
|
- रैखिक ध्रुवित या समतल ध्रुवित प्रकाश को परिभाषित कीजिए। ध्वनि तरंगें ध...
Text Solution
|
- पोलेरॉइड किसका बना होता है ? किस प्रकार पोलेरॉइड पर आपतित अध्रुवित प्र...
Text Solution
|