Home
Class 10
MATHS
In the adjoining figure, seg PQabs()seg ...

In the adjoining figure, seg PQ`abs()`seg DE, `A(DeltaPQF) = 20` sq. uints, PF = 2 DP, then find A `(square DPQE)` by completing the following activity.

Text Solution

Verified by Experts

The correct Answer is:
`= 25 sq.` units
Promotional Banner

Topper's Solved these Questions

  • SIMILARITY

    TARGET PUBLICATION|Exercise Problem Set - 1|19 Videos

  • SIMILARITY

    TARGET PUBLICATION|Exercise Activites for Practice|4 Videos

  • SIMILARITY

    TARGET PUBLICATION|Exercise Practice Set 1.3|9 Videos

  • QUESTION FROM STD. IX

    TARGET PUBLICATION|Exercise Statistics|14 Videos

  • STATISTICS

    TARGET PUBLICATION|Exercise Problem Set-6|21 Videos

Similar Questions

Explore conceptually related problems

In the figure seg PQ|| seg DE, A(DeltaPQF)=20 units PF=2DP ,then find A(square DPQE) by completing the following activity: Activity: A(DeltaPQF)=20 sq units, PF=2DP . Let us assume DP=x :.PF=2x DF=DE+square=square+square=3x In DeltaFDE and DeltaFPQ . /_FDE~=/_square ..........(Corresponding angles) /_FED~=/_square .....(Corresponding angles) :.DeltaFDE~DeltaFPQ .....(AA test) :.(A(DeltaFDE))/(A(DeltaFPQ))=(square)/(square)=((3x)^(2))/((2x)^(2))=9/4 A(DeltaFDE)=9/4A(DeltaFPQ)=9/4xxsquare=square A(squareDPQE)=A(DeltaFDE)-A(DeltaFPQ) =square-square =square

In the adjoining figure, seg EF abs() side AC, AB = 18, AE = 10, BF = 4. Find BC.

In the adjoining figure, seg PS abs() seg QT abs() seg RU, PQ = 6.4, PR = 9.6 and ST = 11, then find the length of SU.

In the adjoining figure, seg XY abs() seg BC, then which of the following statements is true?

In the adjoining figure, square ABCD is inscribed in the sector A-PCQ. The radius of sector C-BXD is 20 cm. Complete the following activity to find the area of shaded region.

In the adoining figure, XY abs() seg AC. If 2 AX = 3 BX and XY = 9, find the value of AC.

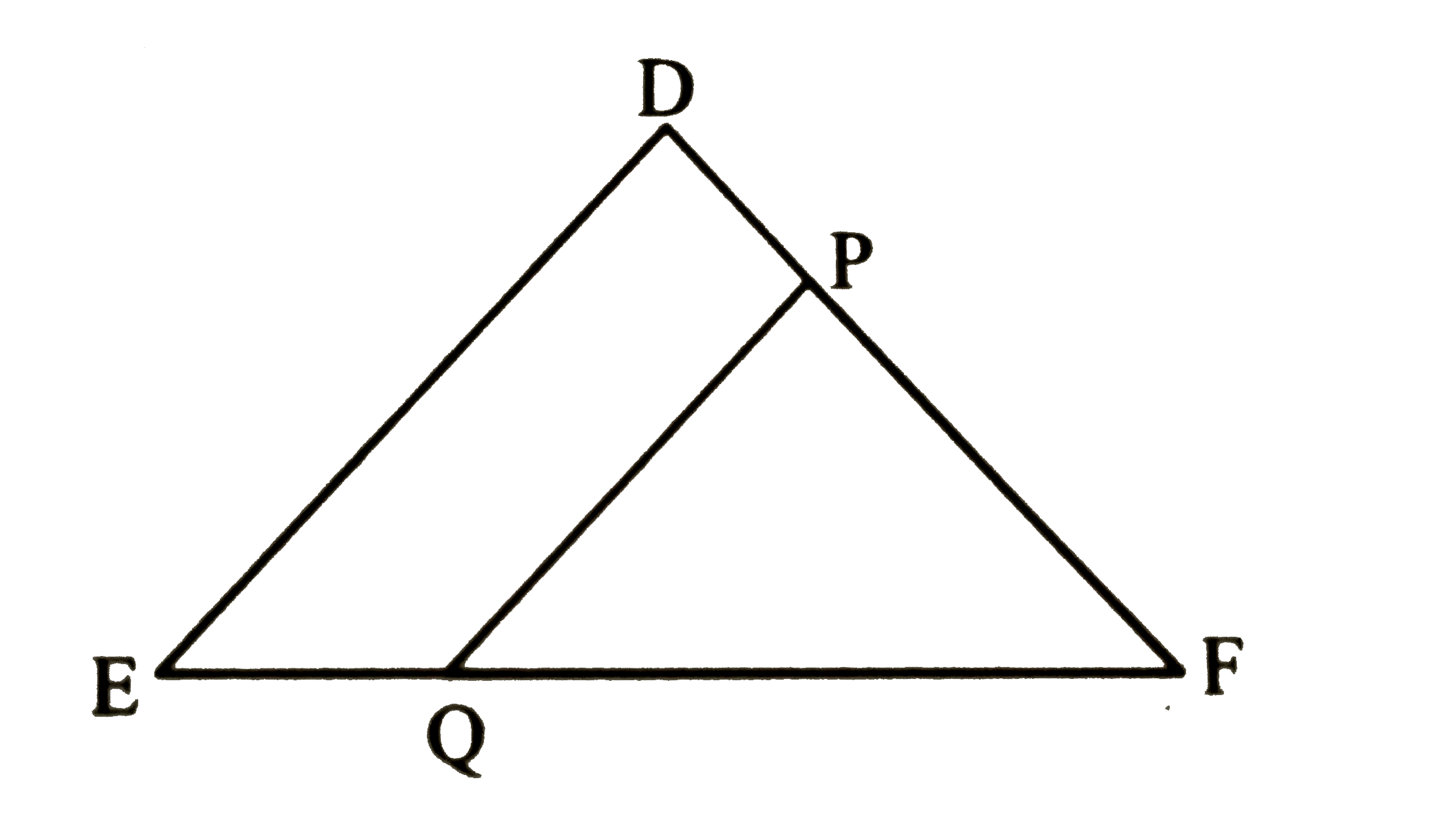
In the adjoining figure, seg XY|| seg AC , IF 3AX=2BX and XY=9 then find the length of AC .

In the given figure, if seg PQ abs() seg BC such that (AP)/(AB) = 2/5 , then (PQ)/(BC) is equal to

(A) Complete any two out of three activites : In the figure , seg SP bot side YK . Seg YT bot side SK . If SP = 6 , YK = 13, YT = 5 and TK = 12 then complete the following activity to find A (Delta SYK ) : A (Delta YTK) The ratio of the areas of the two Deltas is equal to the ratio of the products of their square and the corresponding heights :. (A(Delta SYK))/(A (Delta YTK)) = (square xxSP)/(TK xx TY) = (13 xx 6) /(12 xx square ) = square /square