Text Solution
Verified by Experts
Topper's Solved these Questions
GRAVIATION
PRADEEP|Exercise NCERT|21 VideosGRAVIATION
PRADEEP|Exercise ADDITIONAL EXERCISES|4 VideosGRAVIATION
PRADEEP|Exercise LONG ANSWER QUESTIONS|11 VideosBEHAVIOUR OF PERFECT GAS & KINETIC THEORY
PRADEEP|Exercise Assertion - Reason Type questions|14 VideosKINEMATICS
PRADEEP|Exercise 1 NCERT Comprehension|4 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-GRAVIATION-ADVANCED PROBLEMS FOR COMPETITIONS
- There are three identical point mass bodies each of mass m locted at t...
Text Solution
|
- Show that the object lying at the equator will fly off the surface of ...
Text Solution
|
- A spherical cavity is made inside a sphere of density, d. Its centre l...
Text Solution
|
- If the radius of the earth decreases by 1% without changing its mass, ...
Text Solution
|
- On a planet whose size is the same and mass four times as that of our ...
Text Solution
|
- An artificial satellite is moving in a circular orbit around the earth...
Text Solution
|
- Mass M, of a planet earth is uniformly distributed over a spherical vo...
Text Solution
|
- Determine the speed with which the earth would have to rotate on its a...
Text Solution
|
- The escape speed of a body on the earth's surface is 11.2kms^(-1). A b...
Text Solution
|
- Two equal masses of 6.40 kg are separted by a distance of 0.16 m. A sm...
Text Solution
|
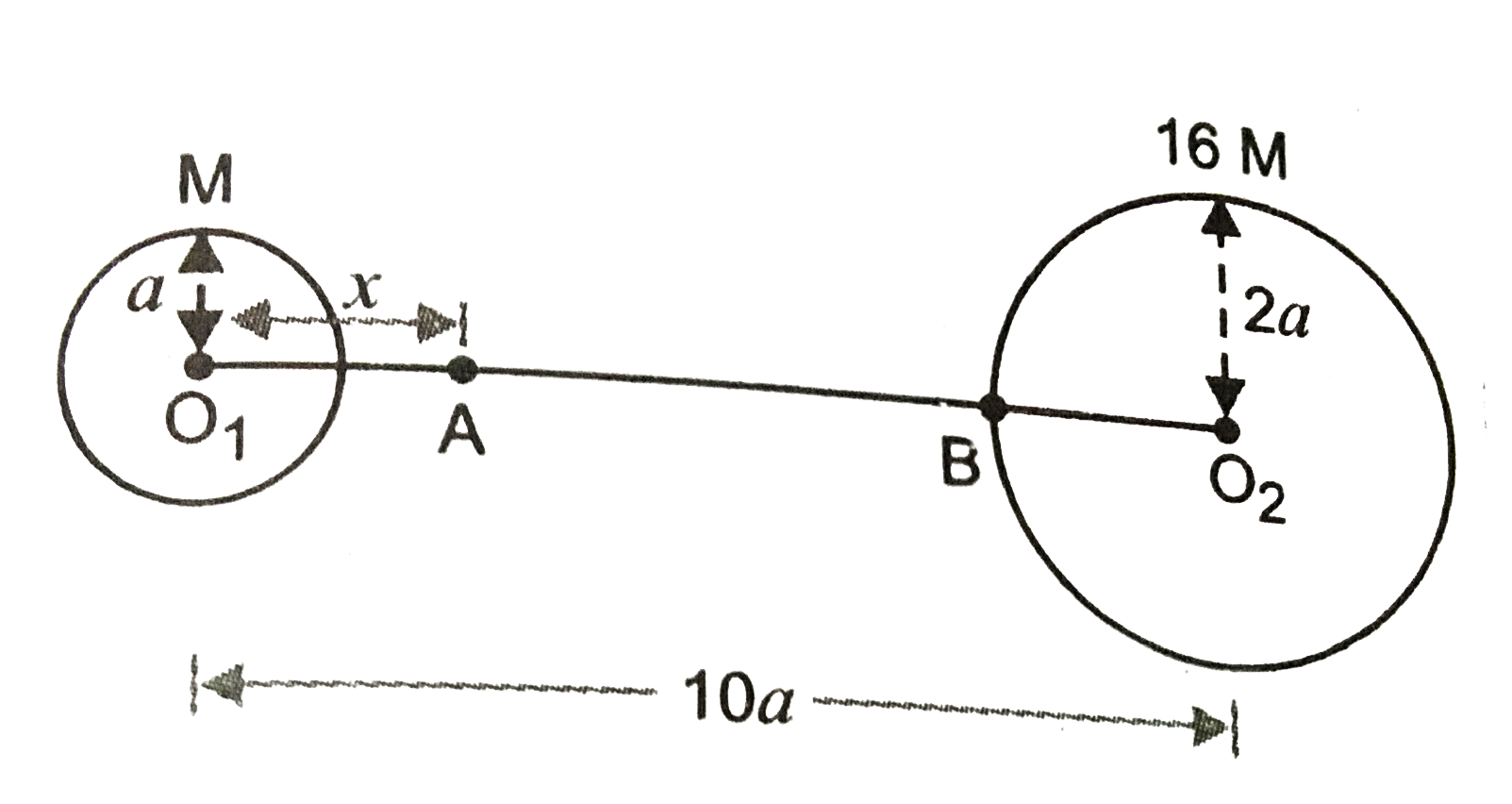
- Distance between the centres of two stars is 10alpha. The masses of th...
Text Solution
|
- The masses and radii of the Earth and the Moon are M1, R1 and M2,R2 re...
Text Solution
|
- A satellite of mass 10 kg is placed initially in a temporary orbit 800...
Text Solution
|
- A non-homogenous sphere of radius R has the following density variatio...
Text Solution
|
- Three equal masses of m kg each are fixed at the vertices of an equila...
Text Solution
|