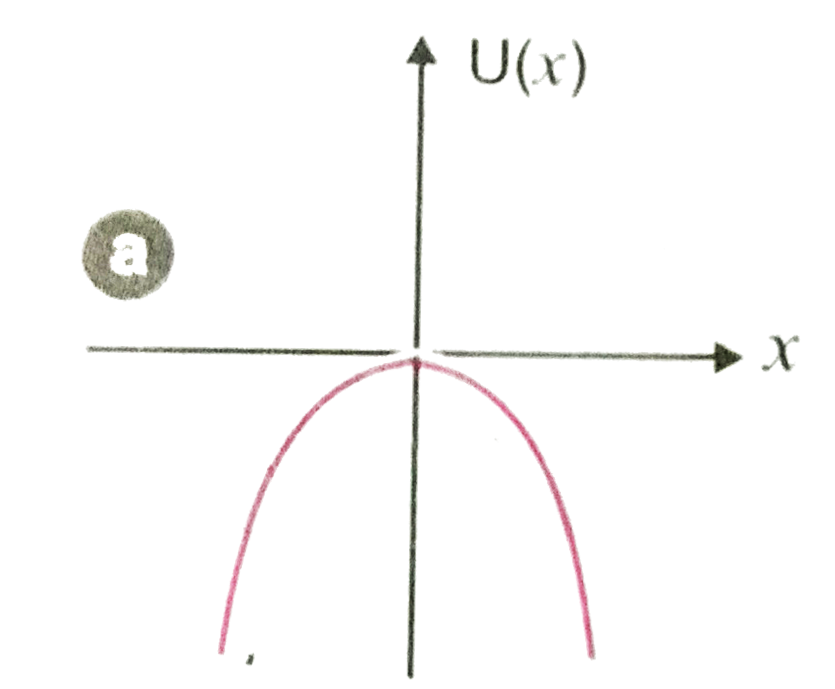
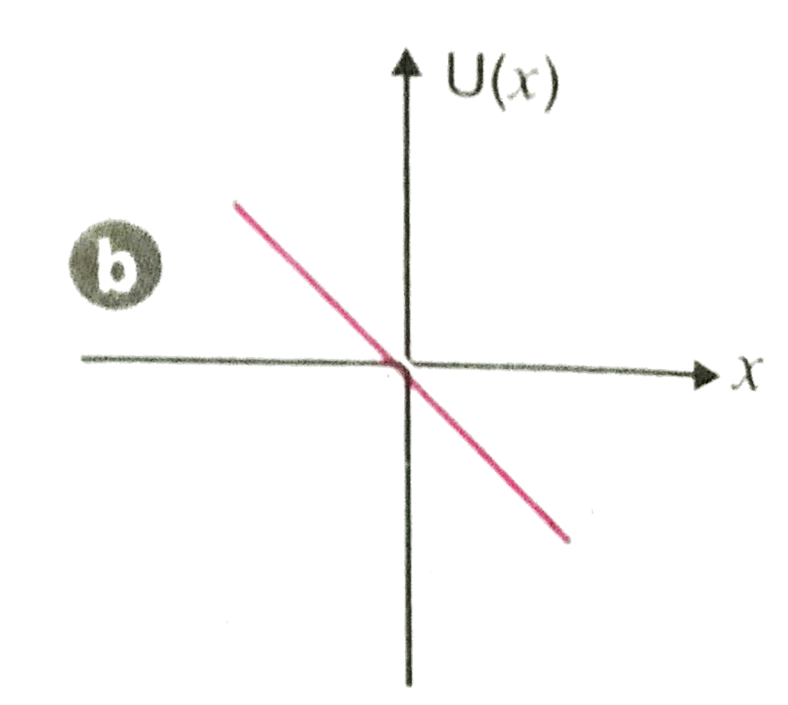
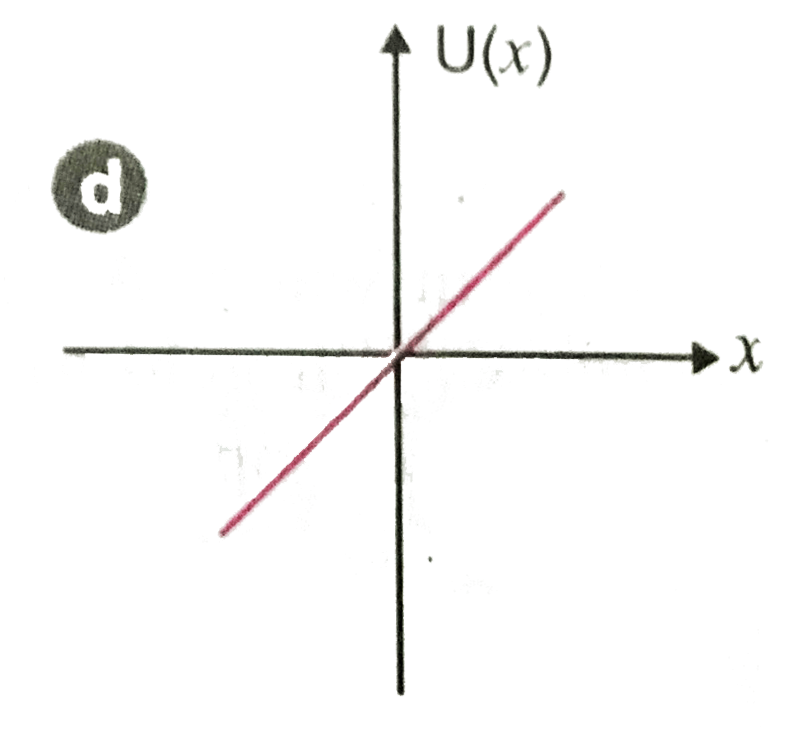
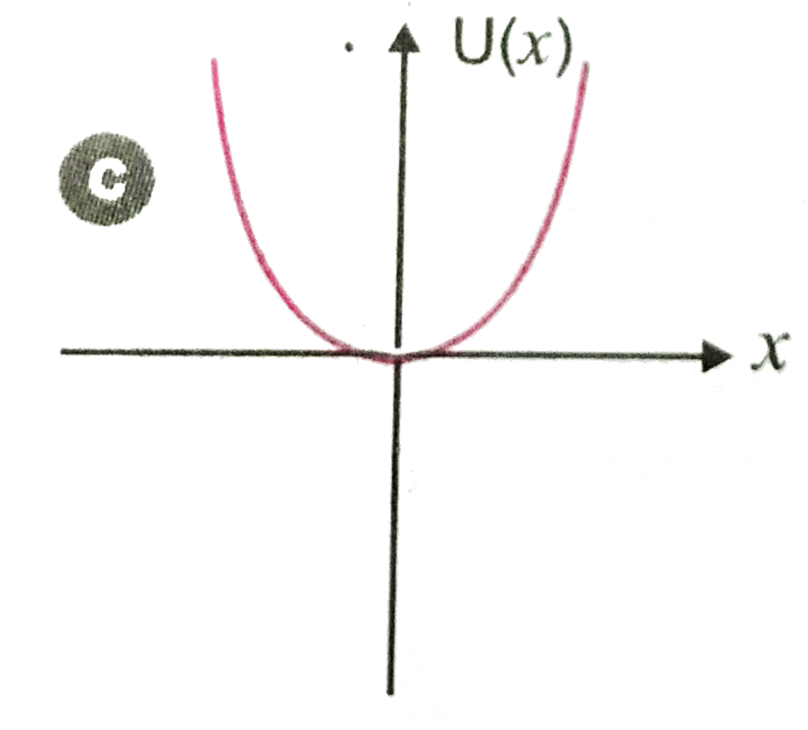A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
PROPERTIES OF BULK MATTER
PRADEEP|Exercise Integer Type Questions|12 VideosPROPERTIES OF BULK MATTER
PRADEEP|Exercise Asseration - Reason Type Question|18 VideosPROPERTIES OF BULK MATTER
PRADEEP|Exercise Multiple choice questions-II|14 VideosPHYSICAL WORLD AND MEASUREMENT
PRADEEP|Exercise Competiton Focus Jee Medical Entrance|18 VideosRAY OPTICS
PRADEEP|Exercise Problem For Practice(a)|25 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-PROPERTIES OF BULK MATTER-Multiple choice questions-I
- Two small drop of mercury, each of radius R coalesce in from a simple ...
Text Solution
|
- Work W is required to form a bubble of volume V from a given solution....
Text Solution
|
- A particle is placed at the origin and a force F=Kx is acting on it (w...
Text Solution
|
- The potential energy function for the force between two atoms in a dia...
Text Solution
|
- A certain number of spherical drops of a liquid of radius r coalesce t...
Text Solution
|
- Assume that a drop of liquid evaporates by decreases in its surface en...
Text Solution
|
- On heating water, bubbles being formed at the bottom of the vessel det...
Text Solution
|
- Under isothermal condition two soap bubbles of radii r(1) and r(2) coa...
Text Solution
|
- The lower end of a capillary tube is dipped in water. Water rises to a...
Text Solution
|
- The lower end of a capillary tube of radius r is placed vertically in ...
Text Solution
|
- A capillary tube of radius r is immersed in water and water rises in t...
Text Solution
|
- A glass capillary tube is of the shape of a truncated cone with an ape...
Text Solution
|
- Water rises to height h in capillary tube. If the length of capillary ...
Text Solution
|
- if a ball of steel (density rho=7.8 g//cm^(3)) attains a terminal velo...
Text Solution
|
- The velocity of small ball of mass M and density d(1) when dropped a c...
Text Solution
|
- A small sphere of mass m is dropped from a great height. After it has ...
Text Solution
|
- The rate of steady volume flow of water through a capillary tube of le...
Text Solution
|
- A lead shot of 1 mm diameter falls through a long colummn of glycerine...
Text Solution
|
- Two solild spheres manufactured of the same material freely fall down ...
Text Solution
|
- A spherical solild of volume V is made of a material of density rho(1)...
Text Solution
|