Text Solution
Verified by Experts
Topper's Solved these Questions
RAY OPTICS
PRADEEP|Exercise Long Answer (b)|15 VideosRAY OPTICS
PRADEEP|Exercise Long Answer (c)|8 VideosRAY OPTICS
PRADEEP|Exercise Short Answer(d)|17 VideosPROPERTIES OF BULK MATTER
PRADEEP|Exercise Multiple choice questions|7 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
PRADEEP|Exercise Assertion- Reason Type questions|20 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-RAY OPTICS-(NCERT)Short Answer
- A short object of length L is placed along the principal axis of a con...
Text Solution
|
- A circular disc of radius 'R' is placed co-axially and horizontally in...
Text Solution
|
- A thin convex lens of focal length 25 cm is cut into two pieces 0.5 cm...
Text Solution
|
- In may experimental set-ups the source and screen are fixed at a dista...
Text Solution
|
- A jar of height h is filled wih a transparent liquid of refractive ind...
Text Solution
|
- A myopic adult has a far point at 0.1 m. His power of accomodation is...
Text Solution
|
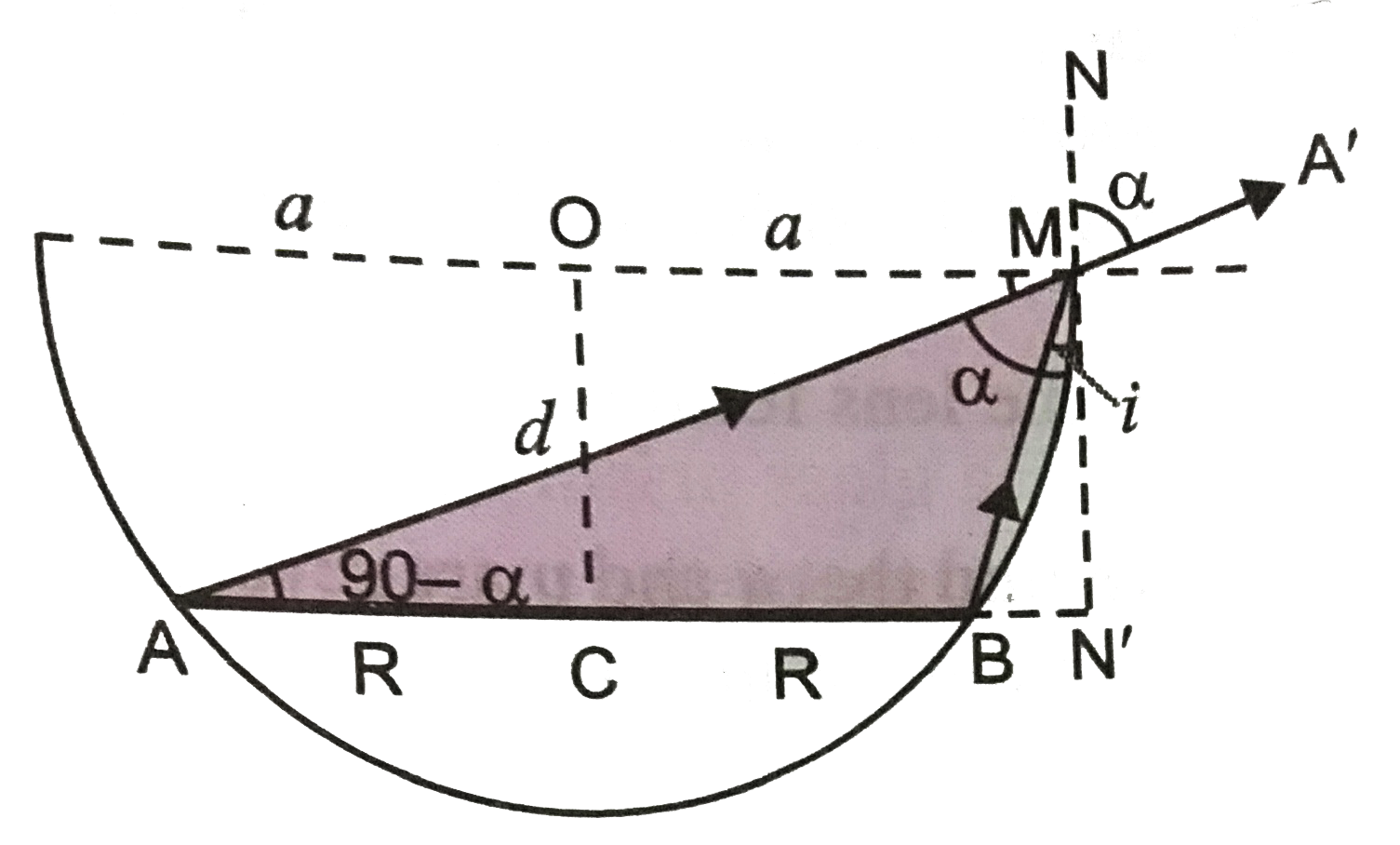 .
.