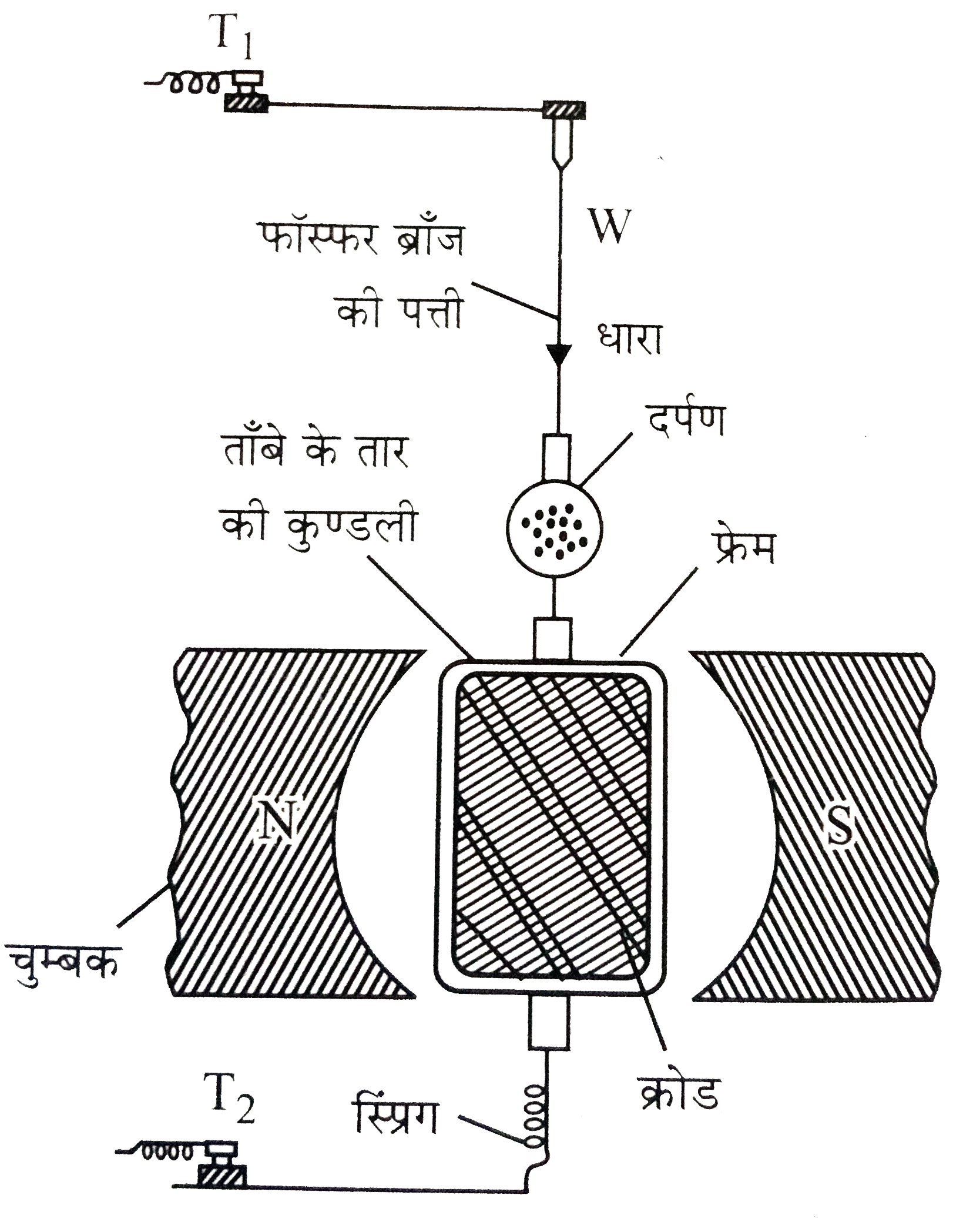संरचना एवं रेखाचित्र - चित्र के अनुसार , इस धारामापी में ताँबे के पतले व पृथक्कृत तार को आयताकार अथवा वृत्ताकार ऐल्युमिनियम के फ्रेस पर लपेटकर एक कुंडली बनायी जाती है । इस कुंडली को फास्फर ब्राँज की पतली पत्ती द्वारा एक मरोड़ी टोपी से प्रबल व स्थायी नाल चुम्बक के ध्रुव खंडों N तथा S के बीच लटकाया जाता है । चुम्बक के ध्रुव अवतल बेलनाकार कटे होते है ,
ताकि इनके बीच चुम्बकीय क्षेत्र त्रिज्यीय हो एवं कुण्डली का तल सदैव चुम्बकीय क्षेत्र के समान्तर हो ।
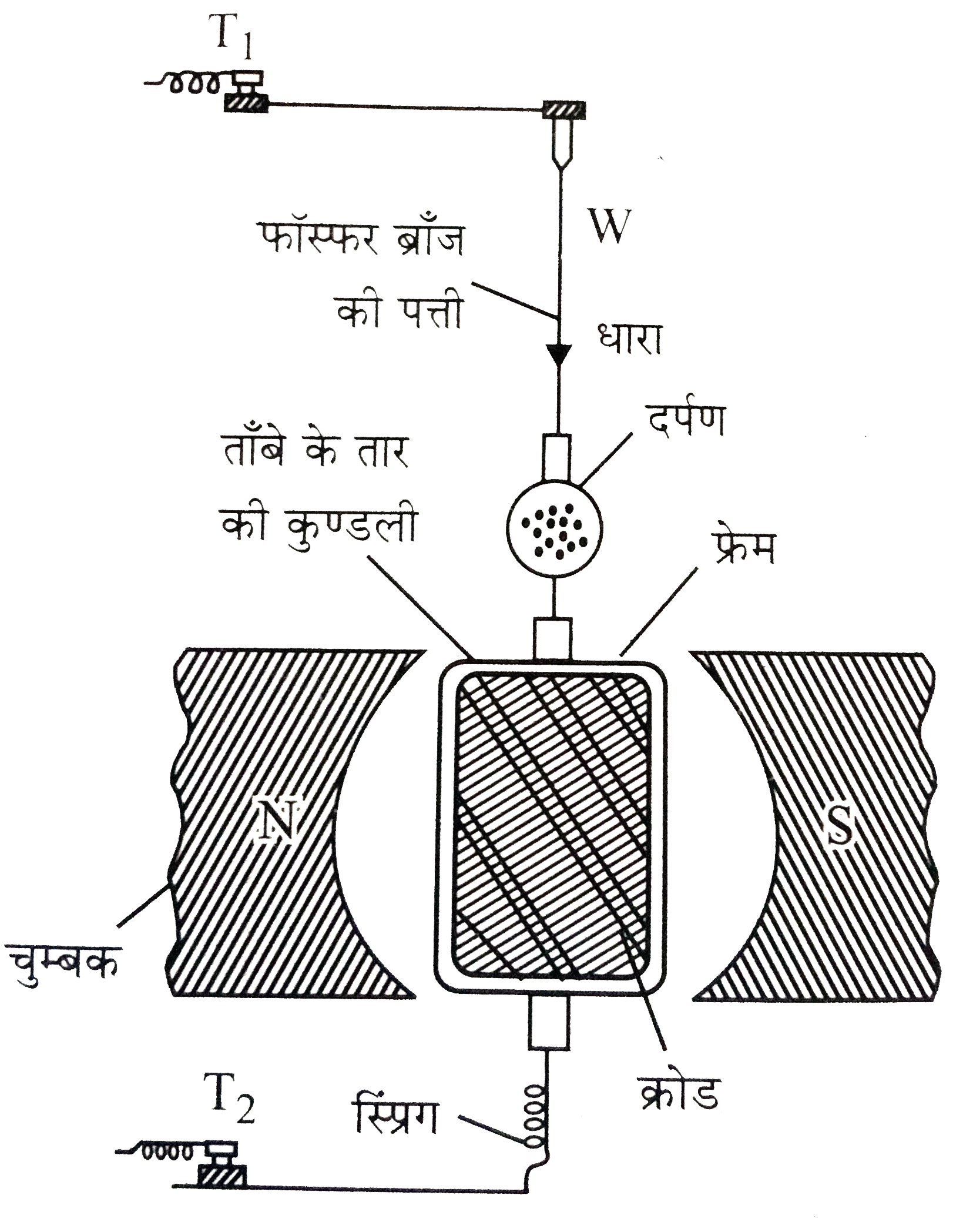
मरोड़ टोपी का सम्बन्ध प्रथम संयोजी पेंच `T_(1)` से होता है तथा कुण्डली का सम्बन्ध स्प्रिंग से होते हुए संयोजी पेंच `T_(2)` से जुड़ा होता है । निलम्बन पत्ती में एक समतल दर्पण लगा होता है जो फॉस्फर ब्राँज के साथ घूमता है । जिससे कुण्डली का विक्षेप ज्ञात किया जा सकता है । जिससे कुण्डली का विक्षेप ज्ञात किया जा सकता है । कुण्डली के अन्दर मुलायम लोहे का क्रोड होता है , जो कुण्डली के ढाँचे के पीछे जुड़ा रहता है, परन्तु कुण्डली को कहीं भी स्पर्श नहीं करता है, क्रोड लेने से चुम्बकीय क्षेत्र प्रबल एवं त्रिज्यीय हो जाता है । यह सम्पूर्ण उपकरण एक अचुम्बकीय पदार्थ के बॉक्स में बंद रहता है, जिससे कि वायु आदि के झोकों का प्रभाव कुण्डली पर न पड़े । बॉक्स के सामने की दीवार काँच की बनी होती है । इसके आधार पर तीन समतलकारी पेंच लगे रहते हैं ।
धारा के सूत्र का निगमन - जब एक धारावाही कुण्डली को किसी एकसमान चुम्बकीय क्षेत्र में स्वतन्त्रता पूर्वक इस प्रकार लटकाते हैं, कि इसका तल चुम्बकीय क्षेत्र के समान्तर रहे तो कुण्डली पर अधिकतम विक्षेपक बलयुग्म लगता है, जो निम्नलिखित होता है-
`tau="NIBA" ` ...(1)
जहाँ N कुण्डली में फेरों की संख्या, I कुण्डली में प्रवाहित धारा, A कुण्डली का क्षेत्रफल तथा B चुम्बकीय क्षेत्र है । इस बलयुग्म के कारण कुण्डली घूमती है, जिससे निलम्बन तार में ऐंठन उत्पन्न होती है । जब ऐंठन बलयुग्म का आघूर्ण , विक्षेपक बलयुग्म के आघूर्ण के बराबर हो जाता है, तो संतुलन अवस्था प्राप्त होती है और कुण्डली ठहर जाती है । यदि संतुलन स्थिति में निलम्बन तार का ऐंठन कोण `phi` हो, तो संतुलन अवस्था में, विक्षेपक बलयुग्म का आघूर्ण = ऐंठन बलयुग्म का आघूर्ण
`"NIAB"=Cphi`
या `I=(C)/(NAB)phi`
यही निलम्बित कुण्डली में बहने वाली धारा का सूत्र है, जिससे यह स्पष्ट है, कि कुण्डली में प्रवाहित धारा ऐंठन कोण के अनुक्रमानुपाती होती है, क्योंकि
`(C)/(NAB)=K=` नियतांक
`I=K phi d`
`rArr I prop phi`
अर्थात धारामापी में प्रवाहित धारा, कुण्डली के विक्षेप के अनुक्रमानुपाती होती हैं ।