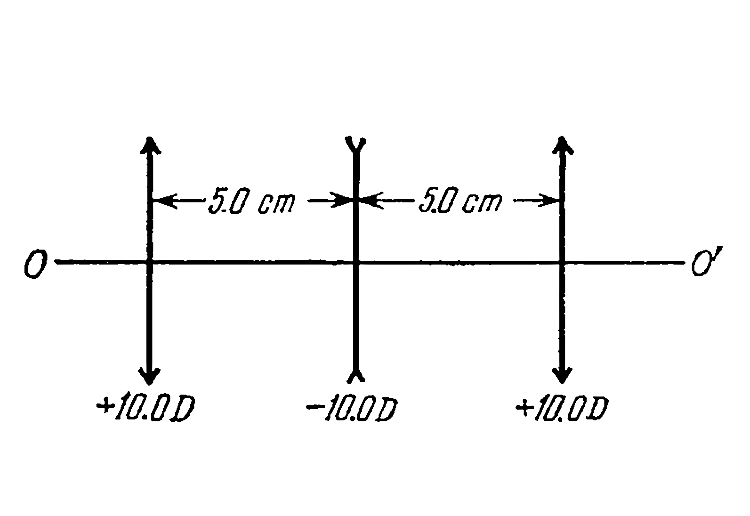
Path of a rays, as it passes through the lens system is as shwon below :
Focal length of all three lenses,
`f = (1)/(10) m = 10 cm`, neglecting their signs.
Applying lens fromula for the first lens, considerting a ray coming from infinity,
`(1)/(s') - (1)/(oo) = (1)/(f)` or, `s' = f = 10 cm`,
and so the position of the image is `5 cm` to the right of the second lens, when only the frist one is present, but the ray again gets refracted while passing through the second, so,
`(1)/(s') - (1)/(5) = (1)/(f) = (1)/(-10)`
or, `s' = 10 cm`, which is now `5 cm` left to the third lens so for this lens,
`(1)/(s'') - (1)/(5) = (1)/(10)` or `(1)/(s') = (3)/(10)`
or, `s'' = 10//3 = 3.33 cm`. from the last lens.
(b) This means that if the object is `x cm` to be left of the first lens on the axis `OO'` then the image is `x` on to the right of the `3rd` (last) ens. Call the lenses `1, 2, 3` from the left and let `O` be the object, `O_(1)` its image by the first lens, `O_(2)` the image of `O_(1)` by the `2nd` lens and `O_(3)`, teh image of `O_(2)` by the third lens.
`O_(1)` and `O_(2)` must be symmetrically located with respect to the lens `L_(2)` and since this lens is concave, `O_(1)` must be at a distance `2|f_(2)|` to be the right of `L_(2)` and `O_(2)` must be `2|f_(2)|` to be the left of `L_(2)`. One can check that this satisfies lens equation for the third lens `L_(3)`
`u =- (2|f_(2)| + 5) =- 25 cm`.
`s' = x, f_(3) = 10 cm`.
Hence `(1)/(x) + (1)/(25) = (1)/(10)` so `x = 16.67 cm`.