लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
पृष्ठीय क्षेत्रफल और आयतन
NOOTAN HINDI|Exercise विविध प्रश्नावली (अतिलघु उत्तरीय प्रश्न)|10 Videosपृष्ठीय क्षेत्रफल और आयतन
NOOTAN HINDI|Exercise लघु उत्तरीय प्रश्न|10 Videosपृष्ठीय क्षेत्रफल और आयतन
NOOTAN HINDI|Exercise ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.4)|5 Videosनिर्देशांक ज्यामिति
NOOTAN HINDI|Exercise बहुविकल्पीय प्रश्न|7 Videosप्रायिकता
NOOTAN HINDI|Exercise बहुविकल्पीय प्रश्न|7 Videos
NOOTAN HINDI-पृष्ठीय क्षेत्रफल और आयतन -ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.5)
- व्यास 3 मिमी वाले ताँबे के एक तार को 12 सेमी लंबे और 10 सेमी व्यास वा...
Text Solution
|
- एक समकोण त्रिभुज , जिसकी भुजाएँ 3 सेमी और 4 सेमी है ( कारण के अतिरिक्त...
Text Solution
|
- एक टंकी , जिसके आंतरिक मापन 150 "सेमी" xx 120 "सेमी" xx110 सेमी है, मे...
Text Solution
|
- किसी महीने के 15 दिनों में , एक नदी की घाटी में 10 सेमी वर्षा हुई । यद...
Text Solution
|
- टीन की बनी हुई एक तेल की कुप्पी 10 सेमी लंबे एक बालन में एक शंकु के छि...
Text Solution
|
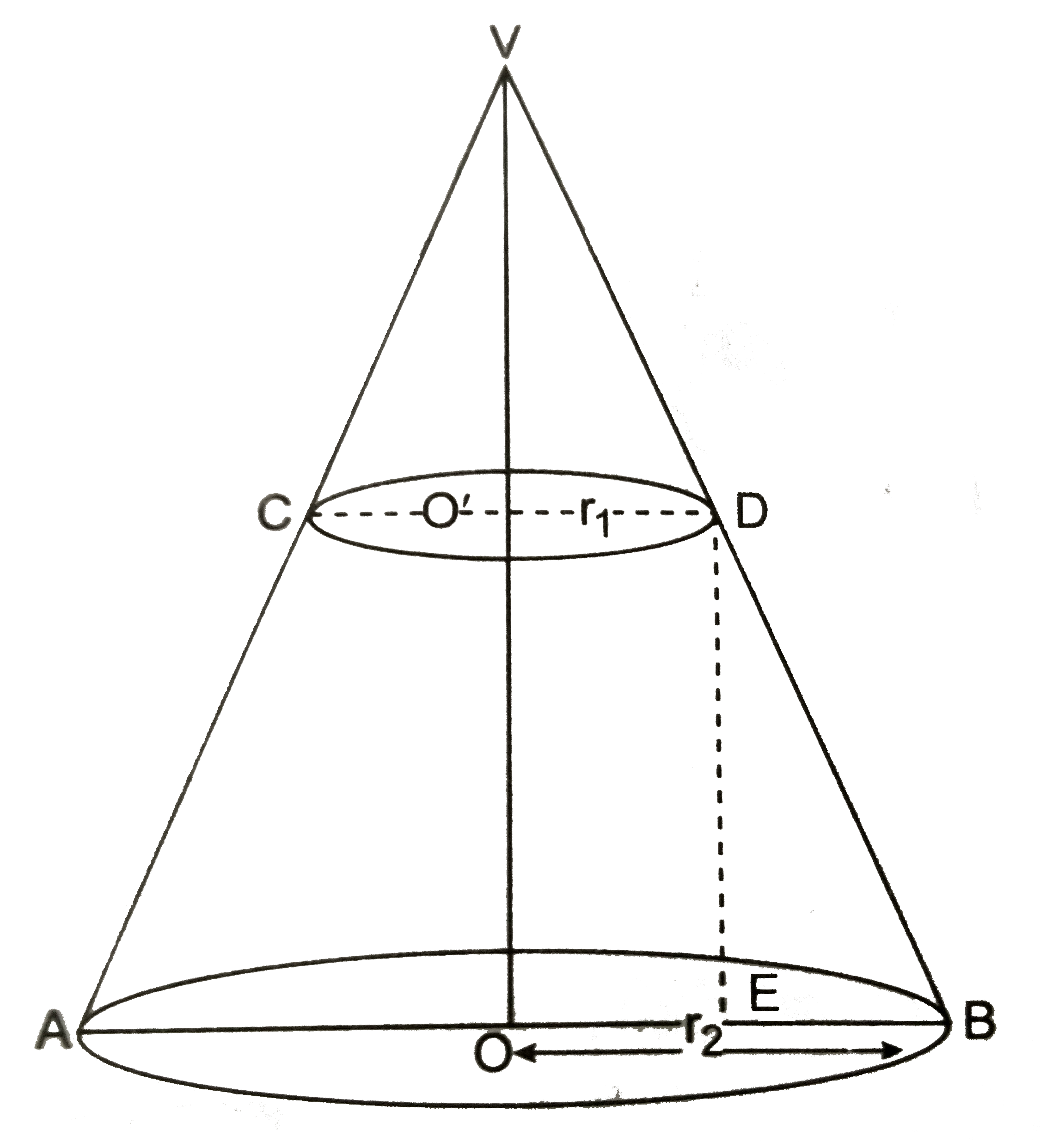
- शंकु के एक छिन्नक के लिए , पूर्व स्पष्ट किए संकेतों का प्रयोग करते हूए...
Text Solution
|
- शंकु के एक छिन्नक के लिए , पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए...
Text Solution
|