लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
NOOTAN HINDI-त्रिभुज -प्रश्नावली 7.2
- एक समद्विबाहु त्रिभुज ABC में, जिसमे AB = AC है, angleA" और "angleC के...
Text Solution
|
- DeltaABC में, AD भुजा BC का लम्ब समद्विभाजक है (देखिए आकृति)। दर्शाइए ...
Text Solution
|
- ABC एक समद्विबाहु त्रिभुज है। भुजाओं AC और AB पर क्रमशः शीर्षलाम्ब BE ...
Text Solution
|
- ABC एक त्रिभुज है जिसमे AC और AB पर खींचे गए शीर्षलाम्ब BE और CF बराबर...
Text Solution
|
- ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज है (देखिए आकृति...
Text Solution
|
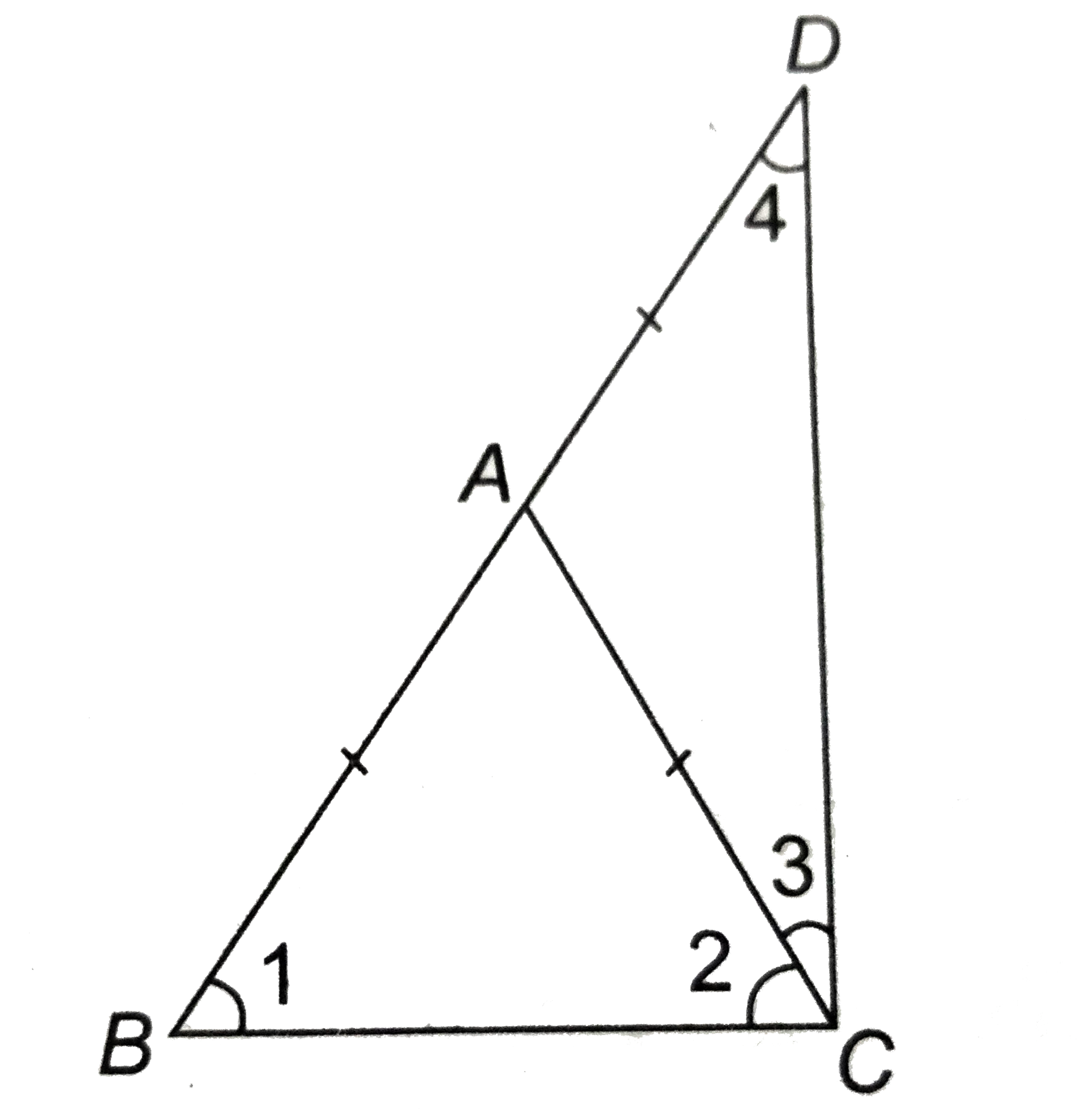
- ABC एक समद्विबाहु त्रिभुज है, जिसमे AB = AC है। भुजा BA बिन्दु D तक इस...
Text Solution
|
- ABC एक समकोण त्रिभुज है, जिसमे angleA=90^(@) और AB = AC है। angleB" और...
Text Solution
|
- दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60^(@) होता है।
Text Solution
|