लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
NOOTAN HINDI-चतुर्भुज-प्रश्नावली 8.2
- ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के ...
Text Solution
|
- ABCD एक समचतुर्भुज है और P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के म...
Text Solution
|
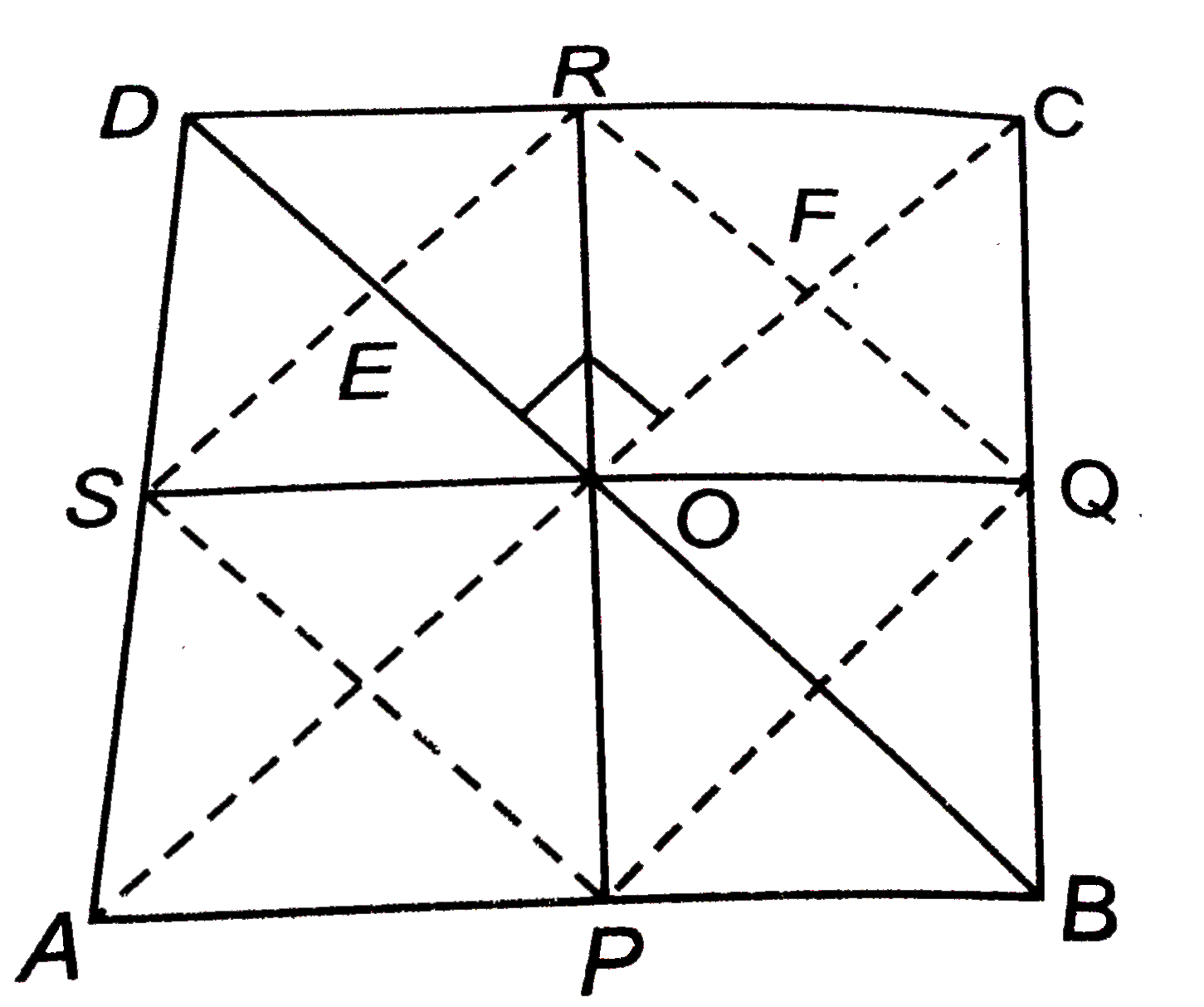
- ABCD एक आयत है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य ...
Text Solution
|
- ABCD एक समलम्ब है जिसमें AB||DC है । साथ ही BD एक विकर्ण है और E भुजा ...
Text Solution
|
- एक समांतर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य बिंद...
Text Solution
|
- दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने व...
Text Solution
|
- ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य बिंदु M से होक...
Text Solution
|