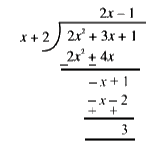Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CHHAYA PUBLICATION-ATOMIC NUCLEUS-CBSE SCANNER
- A 280 days old radioactive shows an activity of 6000 dps, 140 days lat...
Text Solution
|
- Draw a plot of potential energy of a pair of nucleons as a function of...
Text Solution
|
- Define the activity of a given radioactive substance. Write its SI uni...
Text Solution
|
- Draw the plot of binding energy per nucleon (B.E./A) as a function of...
Text Solution
|
- Use this graph to explain the release of energy in both the processes ...
Text Solution
|
- Write the basic nuclear process of neutron undergoing beta-decay . Why...
Text Solution
|
- Why is it found experimentally difficult to detect neutrinos in nuclea...
Text Solution
|
- Define the Activity of a radioactive sample. Write its S.I. unit. A ra...
Text Solution
|
- Derive the mathematical expression for law of radiactive decay for a s...
Text Solution
|
- How is the mean life of a given radiaoactive nucleus related to the d...
Text Solution
|
- A radioactive nucleus 'A' undergoes a series of decays as given below:...
Text Solution
|
- Write the basic nuclear processes underlying beta^+ and beta^- decays.
Text Solution
|
- Four nuclei of an element undergo fusion to form a heavier nucleus , w...
Text Solution
|
- Explain the processes of nuclear fission and nuclear fusion by using t...
Text Solution
|
- A radioactive isotope has a half-life of 10 years. How long will it ta...
Text Solution
|