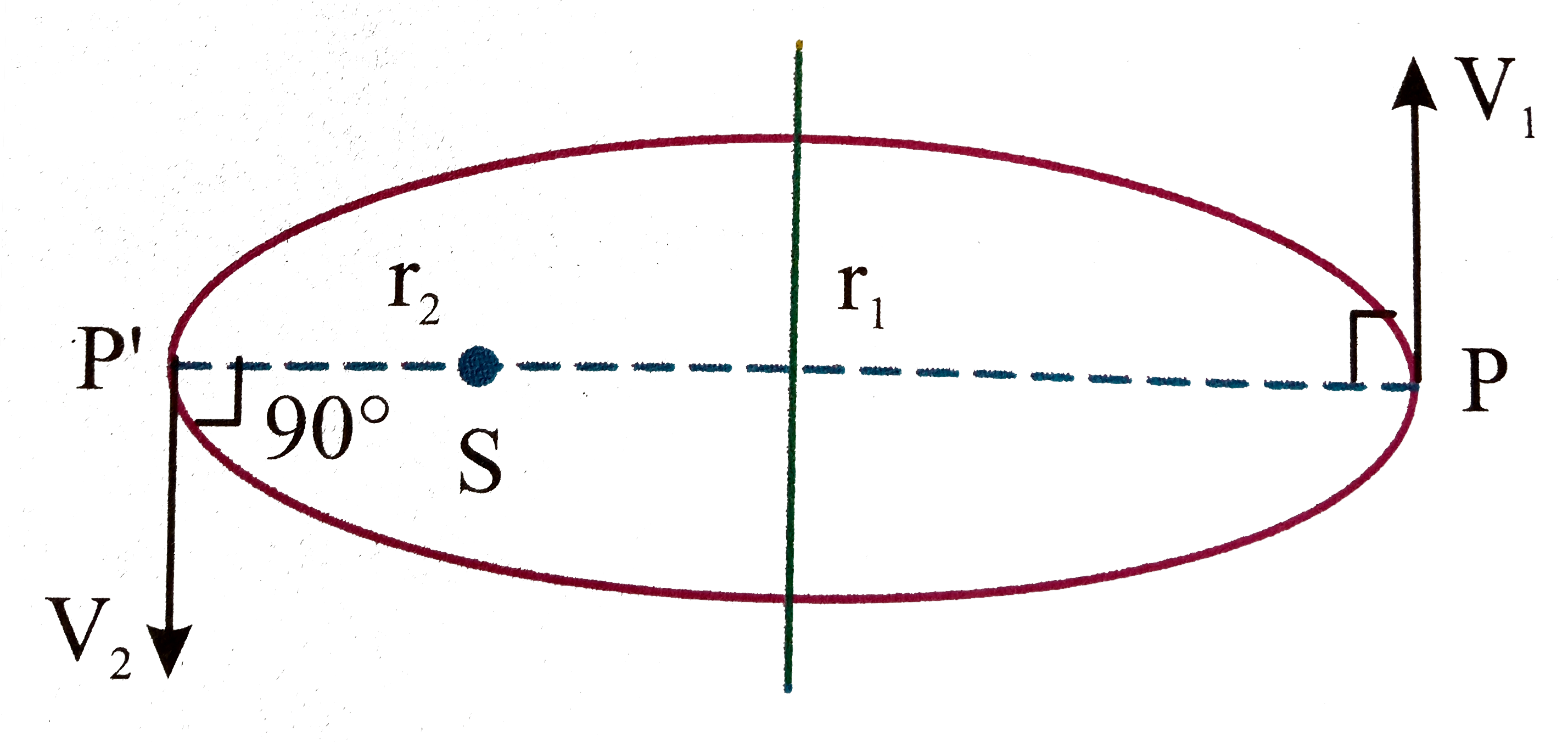
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-GRAVITATION-LEVEL-VI
- Find the potential energy of the gravitational interaction of a point ...
Text Solution
|
- Mass M is distributed uniformly along a line of length 2L. A particle ...
Text Solution
|
- A planet of mass m moves along an ellipse around the sun so that its m...
Text Solution
|
- Inside a uniform sphere of density rho there is a spherical cavity who...
Text Solution
|
- Inside a fixed sphere of radius R and uniform density rho, there is sp...
Text Solution
|
- A ring of radius R = 4m is made of a highly dense material. Mass of th...
Text Solution
|
- A cosmic body A moves to the sun with velocity v(0)(when far from the ...
Text Solution
|
- Two satellite S(1) and S(2) revolve around a planet in coplanar circul...
Text Solution
|
- A particle of mass m is placed on centre of curvature of a fixed, unif...
Text Solution
|
- Given a thin homogenous disc of radius a and mass m(1). A particle of ...
Text Solution
|
- The density of the core a planet is rho(1) and that of the outer shell...
Text Solution
|
- A projectile of mass m is fired from the surface of the earth at an an...
Text Solution
|
- find the velocity of a satellite travelling in an elliptical orbit, wh...
Text Solution
|
- In astronomy order of magnitude estimation plays an important role. Th...
Text Solution
|
- A narrow tunnel is dug across a planet diametrically and a small body ...
Text Solution
|
- If the law of gravitation be such that the force of attraction between...
Text Solution
|
- A small satellite revolves around a heavy planet in a circular orbit. ...
Text Solution
|
- A satellite is orbiting around the earth in an orbitin equatorial plan...
Text Solution
|
- A planet moves aruond the sun in an elliptical orbit such that its kin...
Text Solution
|
- A smooth tunnel is dug along the radius of the earth that ends at the ...
Text Solution
|