A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-NEWTONS LAWS OF MOTION-MULTIPLE ANSWER QUESTIONS
- A book leans against a crate on a table. Neither is moving Which of th...
Text Solution
|
- An iron sphere weighing 10N rests in a V shaped smooth trough whose si...
Text Solution
|
- In the above situation all surface are frictionless system is released...
Text Solution
|
- Two blocks of masses m(1) and m(-2)mgt (m(2)) are connected by massles...
Text Solution
|
- A horizontal bar of mass m(1) Prism of mass m(2) can move as shown. Th...
Text Solution
|
- Which of the following regarding frame of reference is correct ? .
Text Solution
|
- Two masses m(1) and m(2) are connected by light inextensible string pa...
Text Solution
|
- In the arrangement shown in the all contact surfaces are smooth string...
Text Solution
|
- In the shown ,two blocks one of mass 5kg and the other of mass 2kg are...
Text Solution
|
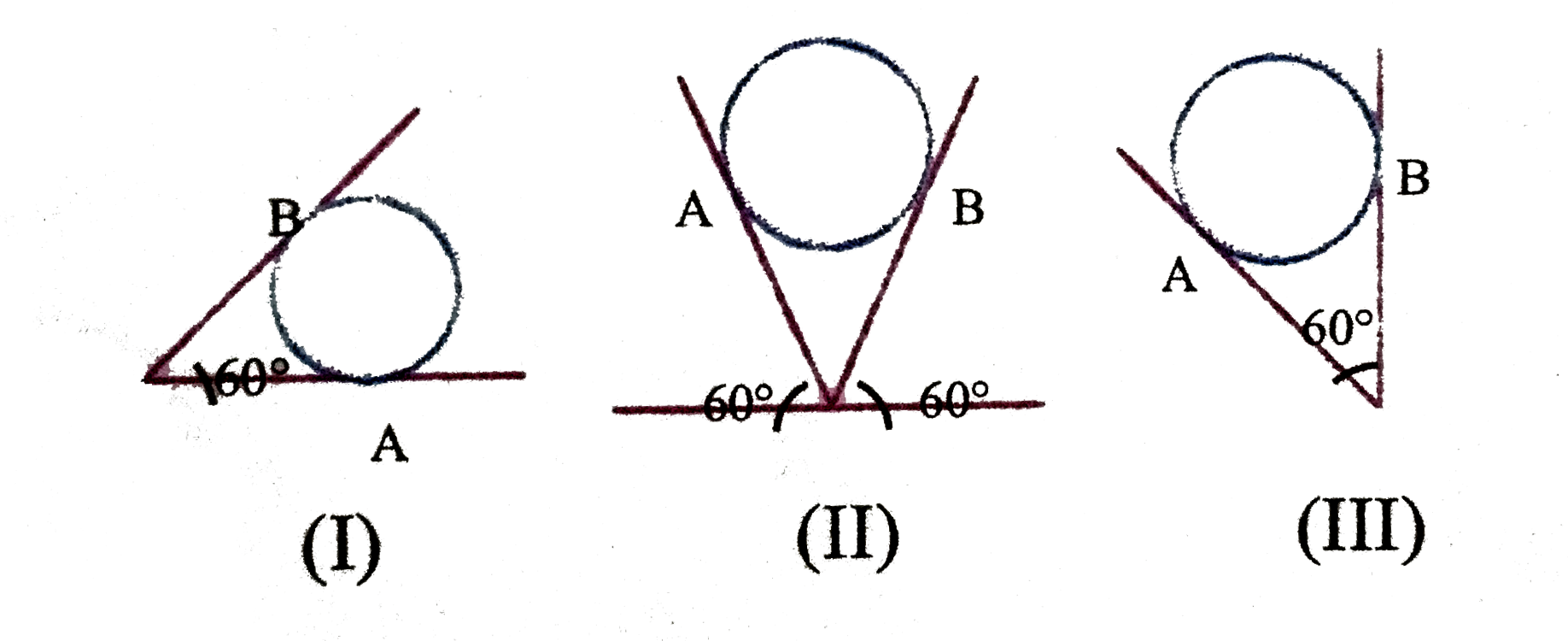 .
.
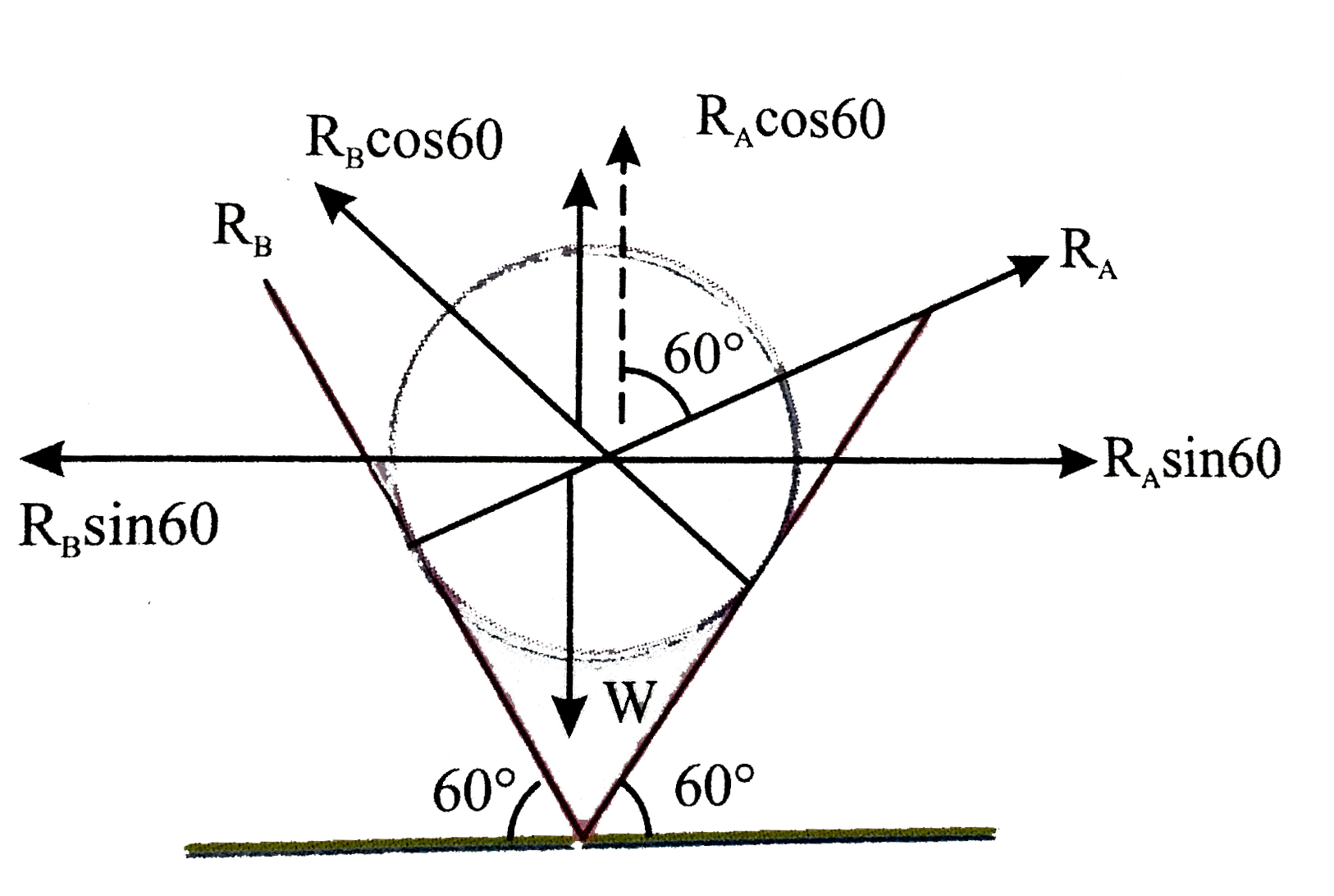
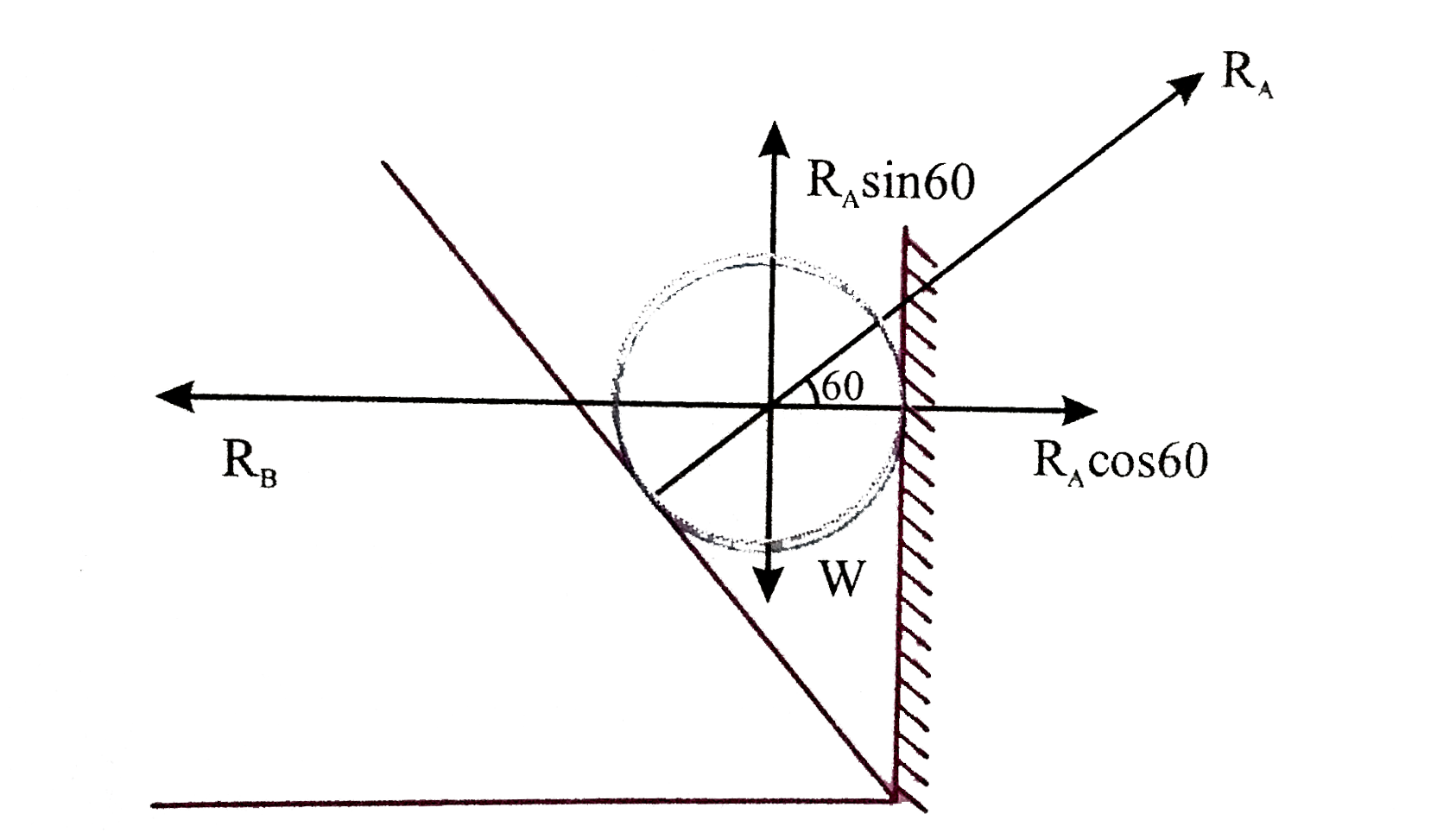 .
.