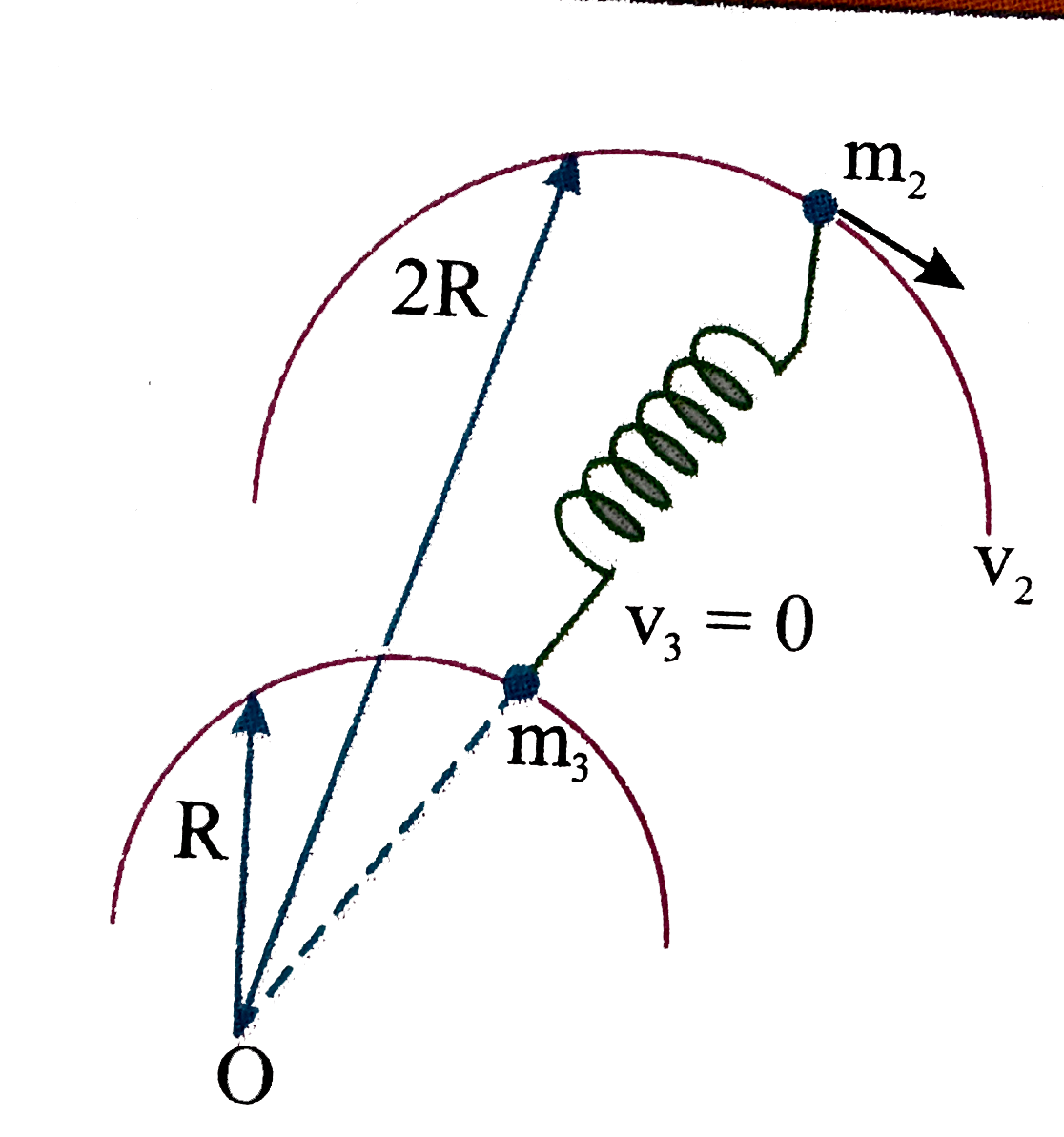A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-SYSTEM OF PARTICLES-Level-V
- A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the ...
Text Solution
|
- A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the ...
Text Solution
|
- There particles each of mass m can slide on fixed frictioless circular...
Text Solution
|
- Three particles each of mass m can slide on fixed friction less circul...
Text Solution
|
- Three particles each of mass m can slide on fixed friction less circul...
Text Solution
|
- In the given figure F=10N, R=1m, mass of the body is 2kg and moment of...
Text Solution
|
- In the given figure F=10N, R=1m, mass of the body is 2kg and moment of...
Text Solution
|
- A plank of length 20 m and mass 1kg is kept on a horizontal smooth sur...
Text Solution
|
- A plank of length 20 m and mass 1kg is kept on a horizontal smooth sur...
Text Solution
|
- A plank of length 20 m and mass 1kg is kept on a horizontal smooth sur...
Text Solution
|
- A plank of length 20 m and mass 1kg is kept on a horizontal smooth sur...
Text Solution
|
- A circular hoop of mass m and radius R rests flat on a horizontal smoo...
Text Solution
|
- A circular hoop of mass m and radius R rests flat on a horizontal smoo...
Text Solution
|
- A circular hoop of mass m and radius R rests flat on a horizontal smoo...
Text Solution
|
- A circular wooden hoop of mass m and radius R rests fiat on a friction...
Text Solution
|
- A circular hoop of mass m and radius R rests flat on a horizontal smoo...
Text Solution
|
- A uniform rod of mass m is supported on two rollers each of mass m//2...
Text Solution
|
- A uniform rod of mass m is supported on two rollers each of mass m//2...
Text Solution
|
- A uniform rod of mass m is supported on two rollers each of mass m//2...
Text Solution
|
- One end of an ideal spring of unstreched length l(O)=1m, is fixed on a...
Text Solution
|