A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MECHANICAL PROPERTIES OF FLUIDS
NARAYNA|Exercise integer Type Questions|25 VideosMECHANICAL PROPERTIES OF FLUIDS
NARAYNA|Exercise Level 1 (H.W)|55 VideosMECHANICAL PROPERTIES OF FLUIDS
NARAYNA|Exercise Paragraph Type Questions|5 VideosMATHEMATICAL REVIEW & PHYSICAL WORLD
NARAYNA|Exercise C.U.Q|13 VideosMECHANICAL PROPERTIES OF SOLIDS
NARAYNA|Exercise LEVEL-II (H.W)|24 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-MECHANICAL PROPERTIES OF FLUIDS-Single Answer Questions
- In the arrangement as shown, m(B)=3m, density of liquid is rho and den...
Text Solution
|
- In the arrangement shown two liquids of density rho and 2rho are fille...
Text Solution
|
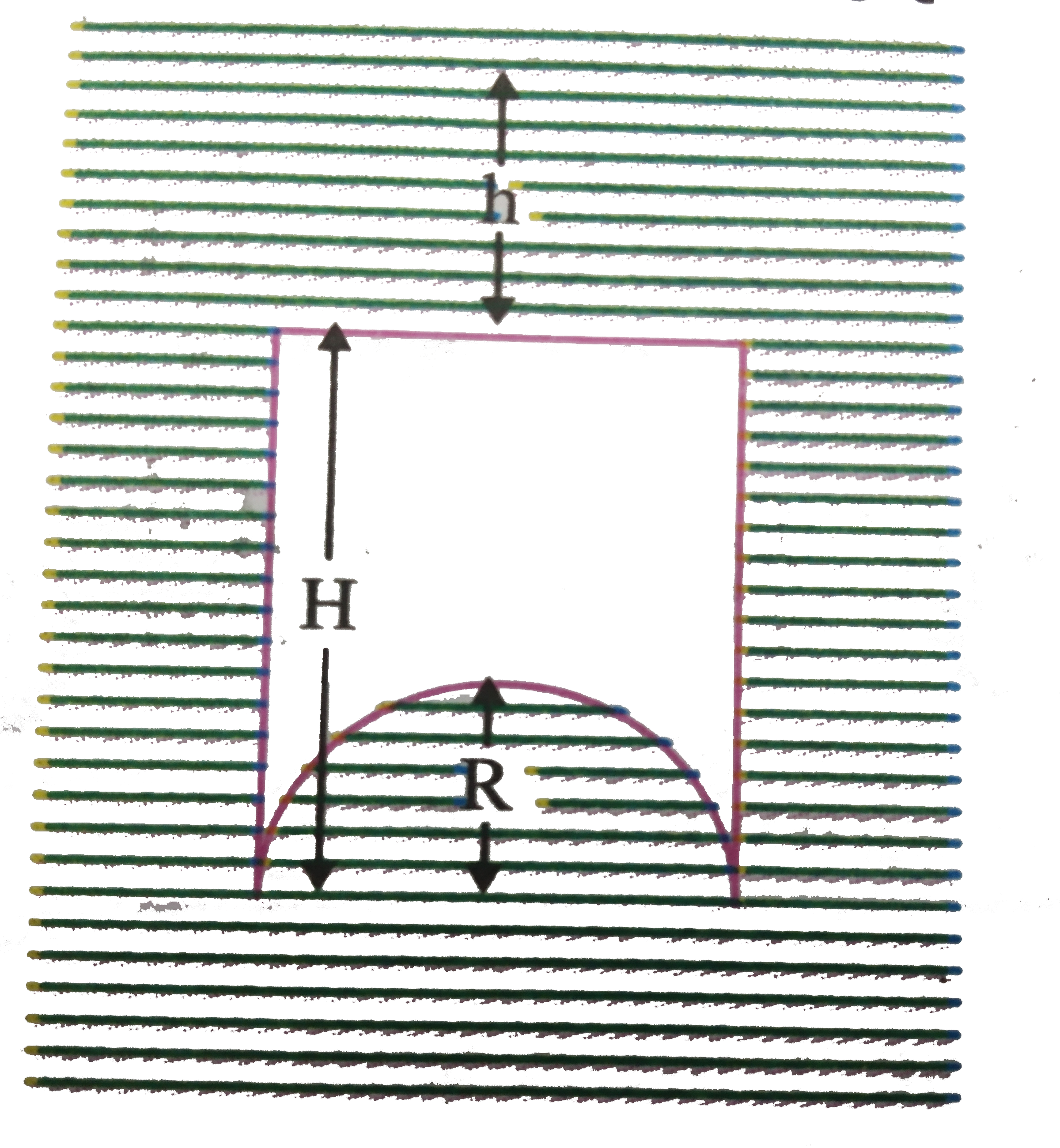
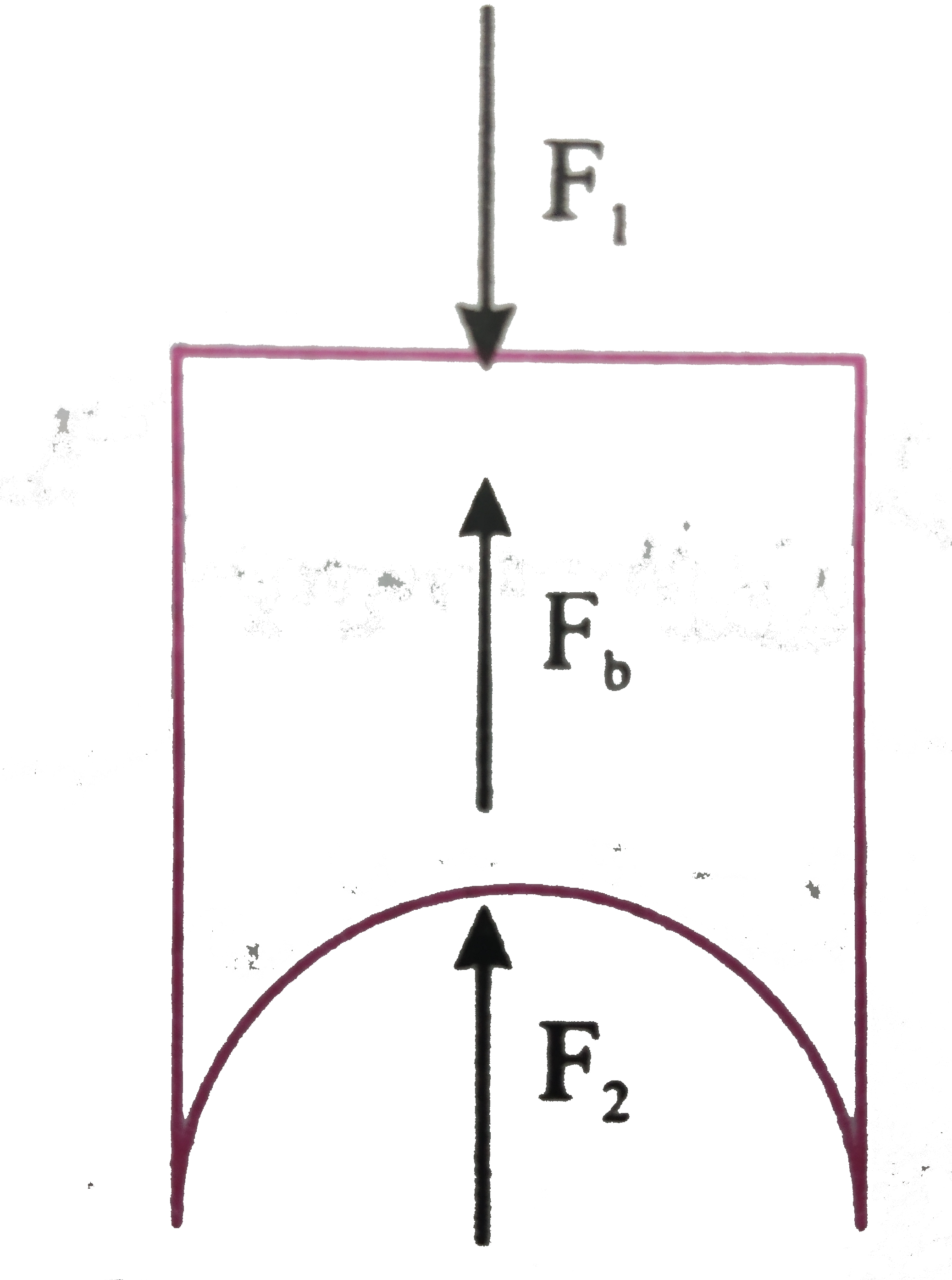
- A cylinder of radius R, height H and density simga has a hemispherical...
Text Solution
|
- A cylindrical container of radius 'R' and height 'h' is completely fil...
Text Solution
|
- A marble of mass x and diameter 2r is gently released in a tall cylind...
Text Solution
|
- A small metal ball of diameter 4 mm and density 10.5 g//cm^(3) in drop...
Text Solution
|
- A sphere of brass released in a long liquid column attains a terminal ...
Text Solution
|
- Between a plate of area 100 cm^(2) and another plate of area 100 m^(2)...
Text Solution
|
- A spherical ball falls through a viscous medium with terminal velocity...
Text Solution
|
- Neglecting the density of air, the terminal velocity obtained by a rai...
Text Solution
|
- Water is flowing in a river. If the velocity of a layer at a distance ...
Text Solution
|
- A horizontal plate (10cmxx10cm) moves on a layer of oil of thickness 4...
Text Solution
|
- A liquid is flowing through a narrow tube. The coefficient of viscosit...
Text Solution
|
- Find the terminal velocity of solid sphere of radius 0.1 m moving in a...
Text Solution
|
- Eight equal drops of water each of radius r=2mm are falling through ai...
Text Solution
|
- At 20^(@)C to attain the terminal velocity how fast will an aluminium ...
Text Solution
|
- Water flows at a speed of 6 cms^-1 through a tube of radius 1 cm. coe...
Text Solution
|
- A metal sphere of radius 1 mm and mass 50 mg falls vertically in glyce...
Text Solution
|
- A liquid of density 900(kg)/(m^(3)) is filled in a cylindrical tank of...
Text Solution
|
- If the terminal speed of a sphere of gold (density =19.5kg//m^3) is 0....
Text Solution
|