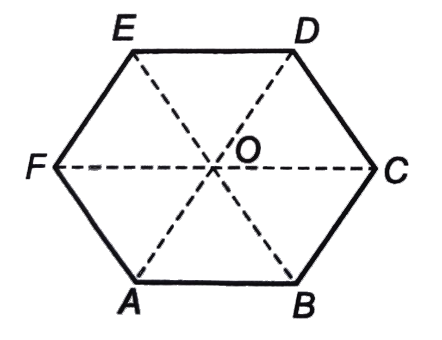
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-VECTORS-Excercises
- Five equal forces of 10 N each are applied at one point and all are ly...
Text Solution
|
- Forces proportional to AB , BC and 2 CA act along the slides of a tria...
Text Solution
|
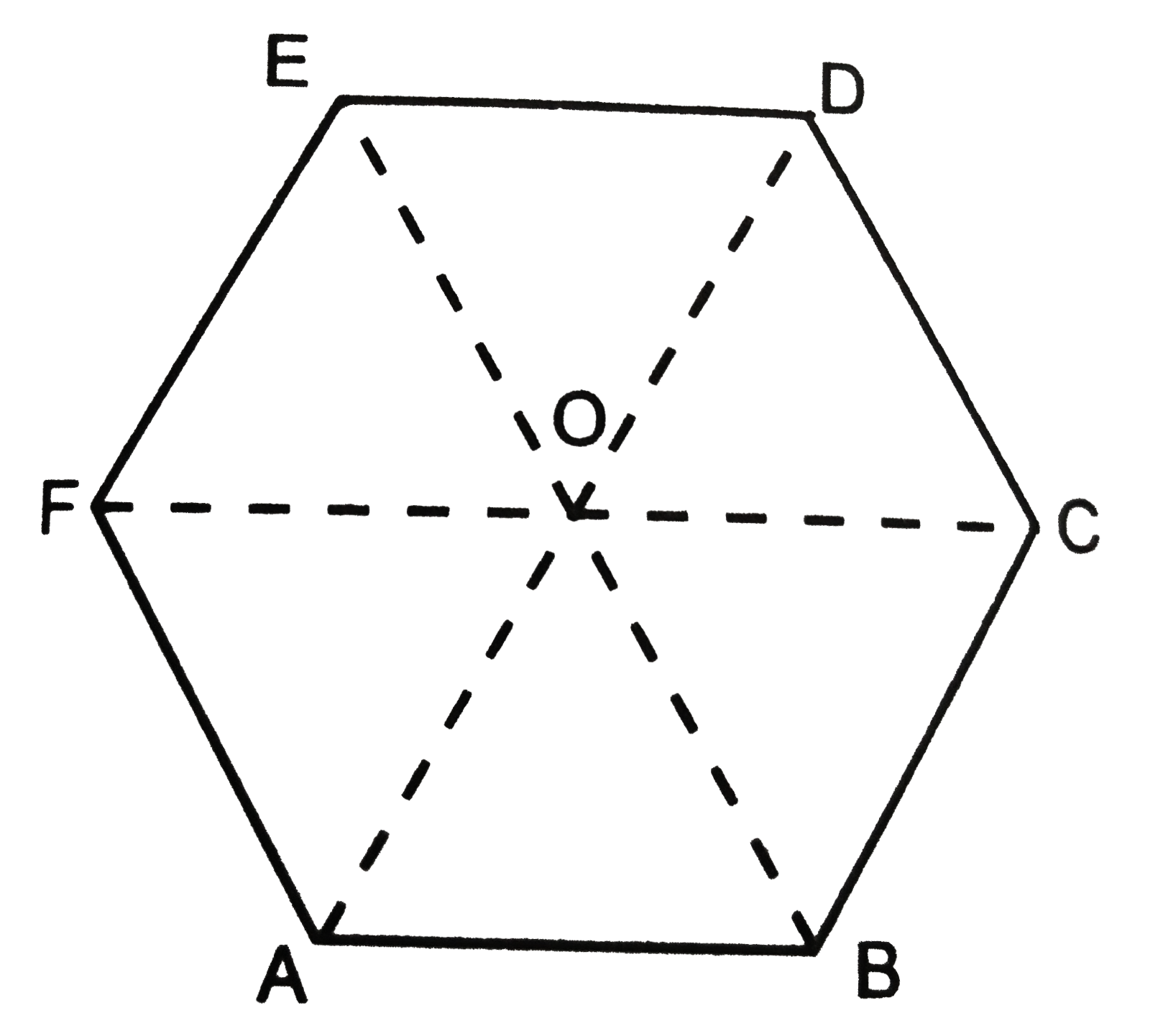
- ABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of ...
Text Solution
|
- A truck travelling due to north at 20m s^(-1) turns west and travels a...
Text Solution
|
- A particle moves towards east with velocity 5m//s. After 10 seconds it...
Text Solution
|
- The length of second's hand in watch is 1 cm. The change in Velocity o...
Text Solution
|
- Aparticle moves with a speed v changes direction by an angle theta, w...
Text Solution
|
- Let the angle between two non - zero vectors vec(A) and vec(B) be 120^...
Text Solution
|
- The component of a vector is
Text Solution
|
- One of the two rectangular components of a force is 20 N and it makes ...
Text Solution
|
- While travelling from one station to another , a car travels 75 "km no...
Text Solution
|
- A person moves 30 m north, then 30 m est, then 30sqrt(2) south-west. H...
Text Solution
|
- Find the resultant of the three vectors vec(OA), vec(OB) and vec(OC) s...
Text Solution
|
- Three forces acting on a body are shown in figure. To have the resulta...
Text Solution
|
- The x- component of the resultant of several vectors (i) is equal to...
Text Solution
|
- A hall has the dimensions 10 m xx 12 m xx 14 m. A fly starting at one ...
Text Solution
|
- If a unit vector is represented by 0.5 hat(i) + 0.8 hat(j) + c hat(k) ...
Text Solution
|
- If vec(A) = 3 hat(i) - 4 hat(j) and vec(B) = 2 hat(i) + 16 hat(j) then...
Text Solution
|
- If a particle moves from the point A(1 , 2 , 3) to the point B( 4 , 6 ...
Text Solution
|
- The unit vector parallel to the resultant of the vectors vec(A) = hat(...
Text Solution
|
 .
.