Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-FRICTION-Exercises
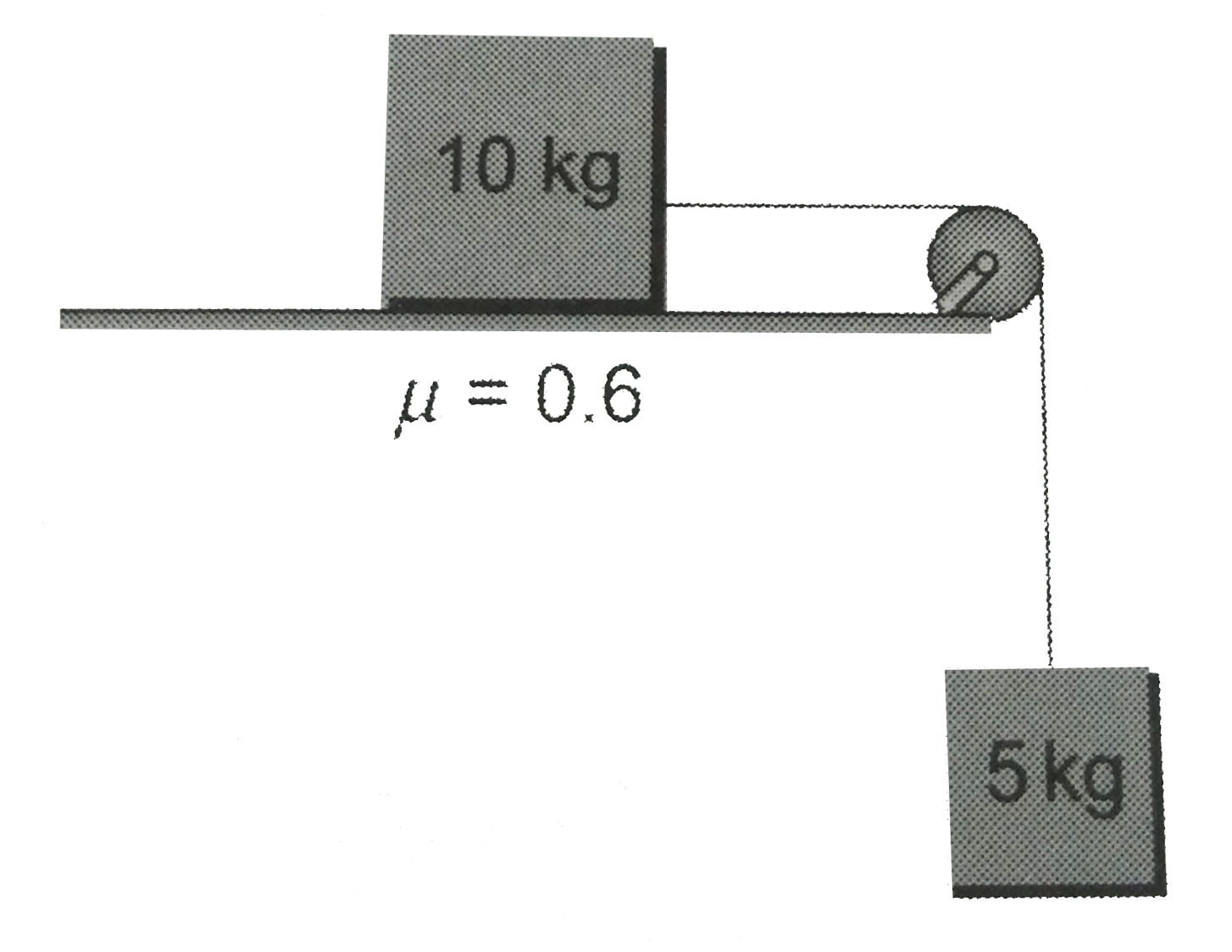
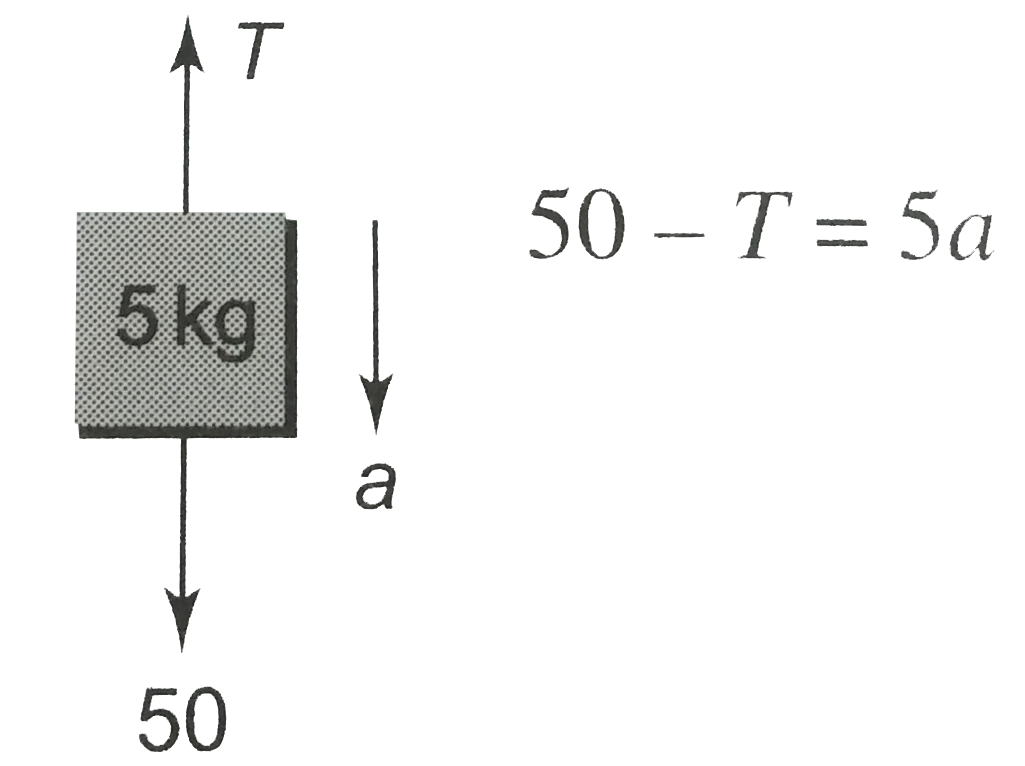
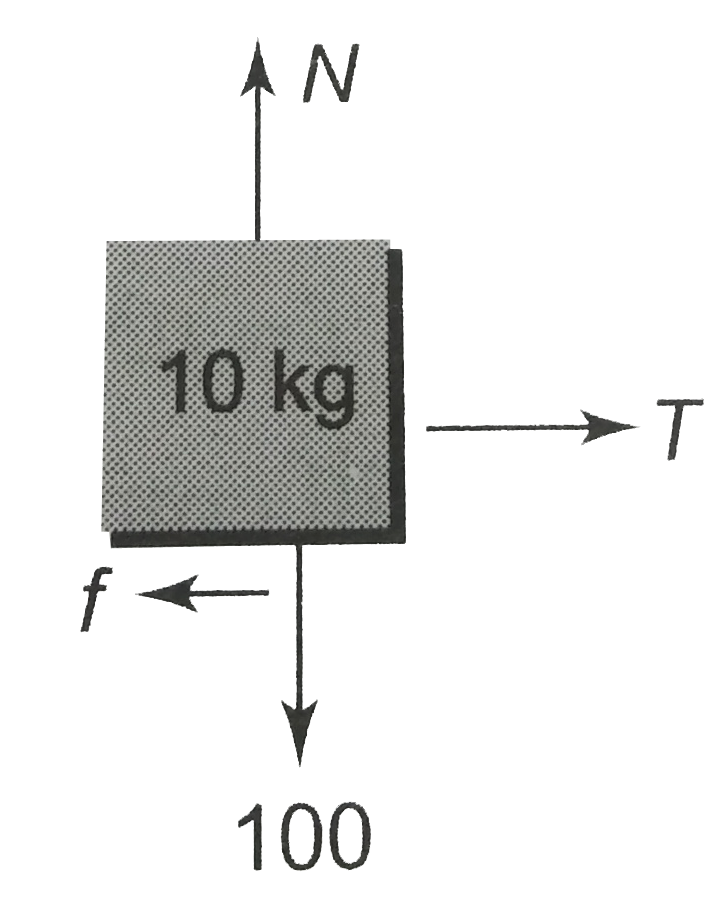
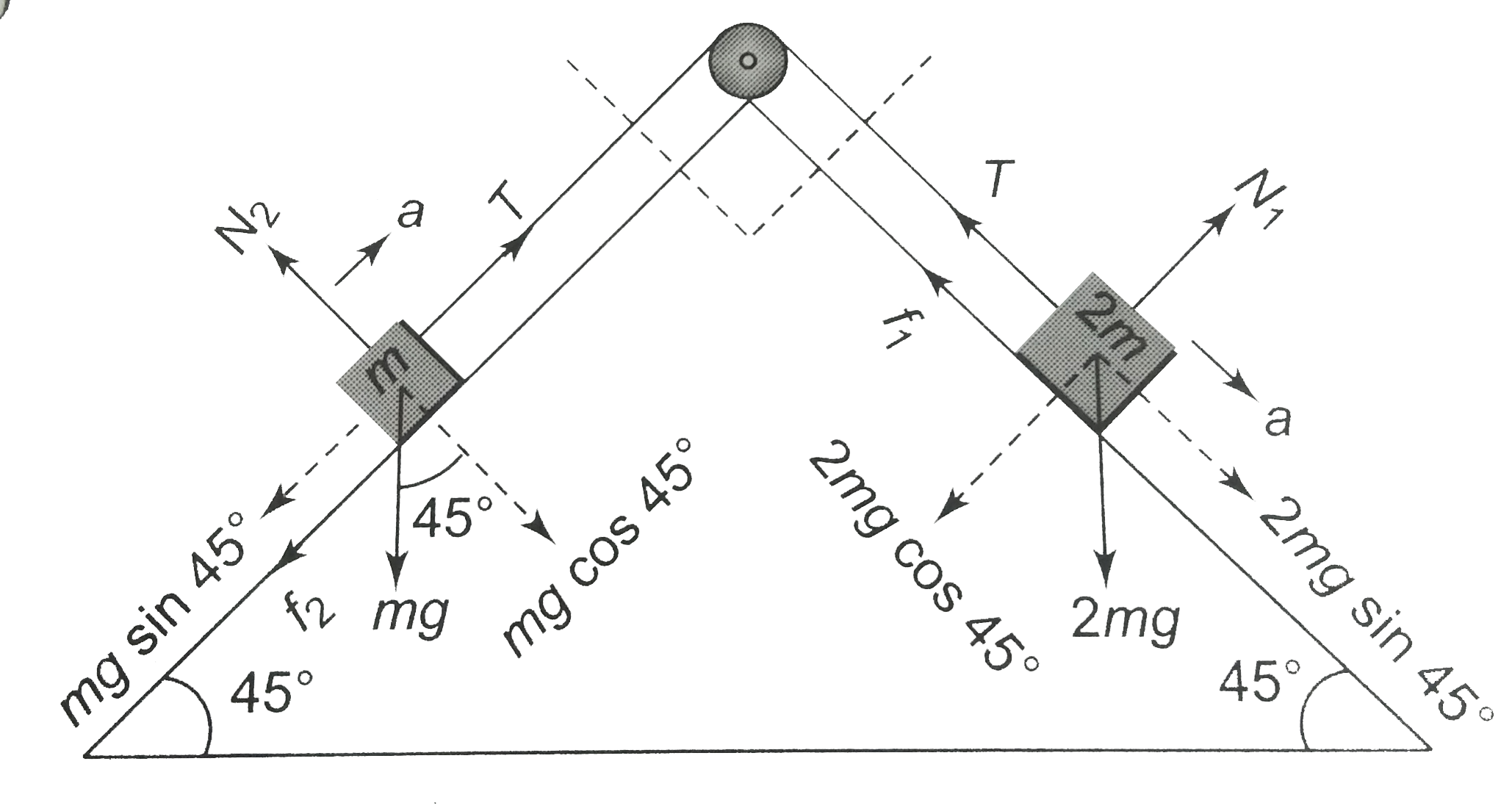
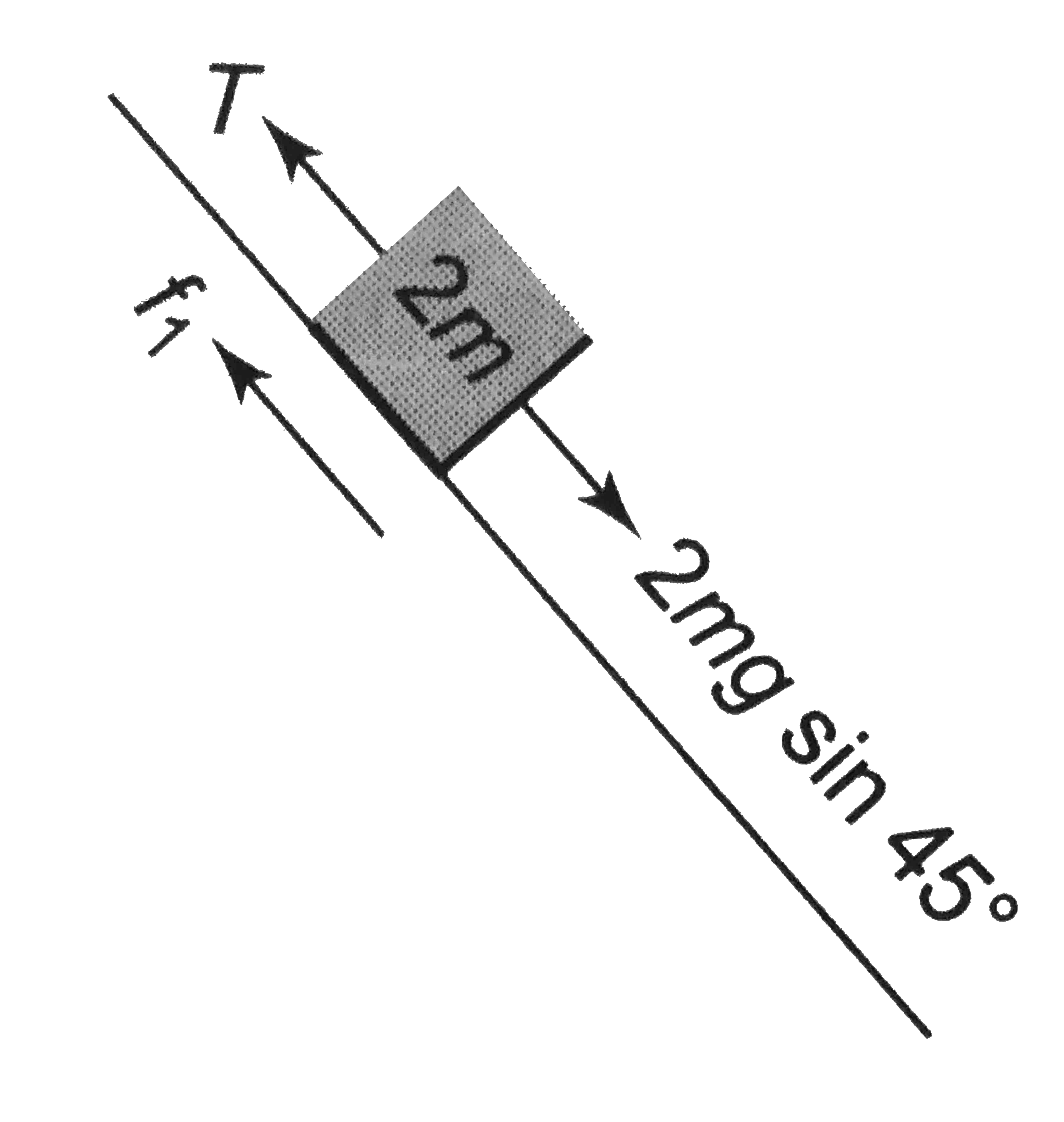
- Find the acceleration and tension in the string in the following cases...
Text Solution
|
- Choose the correct option
Text Solution
|
- Consider a car moving on a straight road with a speed of 100m//s. The ...
Text Solution
|
- A car is moving along a stight horizontal road with a speed v(0) . If ...
Text Solution
|
- Two cars of unequal masses use similar tyres. If they are moving at th...
Text Solution
|
- An ice cube is kept on an inclined plane of angle 30^(@). The coeffici...
Text Solution
|
- Starting from rest , a body slides down at 45^(@) inclined plane in tw...
Text Solution
|
- A smooth block is released at rest on a 45^@ incline and then slides a...
Text Solution
|
- A block is released from the top of an inclined plane of inclination t...
Text Solution
|
- The upper half of an inclined plane of inclination 45^(@) is perfectly...
Text Solution
|
- A body is sliding down an inclined plane (mu = (1)/(2)). If the normal...
Text Solution
|
- A ball is thrown vertically with some velocity . A constant air resist...
Text Solution
|
- In an imaginary atmosphere, the air exerts a small force F on any part...
Text Solution
|
- Two objects A and B are thrown upward simultaneously with the same spe...
Text Solution
|
- A ball is thrown vertically upward with speed 10 m//s and it returns t...
Text Solution
|
- A particle is projected up a rough inclined plane of inclination theta...
Text Solution
|
- A particle is projected up a 37^(@) rough incline with velocity v(0). ...
Text Solution
|
- As shown in the figure , the friction force acting on the block is
Text Solution
|
- The friction force acting on the block at time t = 4 s will be
Text Solution
|
- A block of mass 2kg rests on a rough inclined plane making an angle of...
Text Solution
|
- Consider the situation as shown in the figure. Choose the correct opti...
Text Solution
|