Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-FLUID MECHANICS-Exercises
- A cylindrical tank 1 m in radius rests on a platform 5 m high. Initial...
Text Solution
|
- In making an alloy, a substance of specific gravity s(1) and mass m(1)...
Text Solution
|
- A liquid can easily change its shape but a solid can not because
Text Solution
|
- Consider the equations P=Lim(/\srarr0)F/(/\S) and P1-P2=rhogz In a...
Text Solution
|
- The three vessels shown in figure have same base area. Equal volumes o...
Text Solution
|
- Equal mass of three liquids are kept in three identical cuylindrical v...
Text Solution
|
- Figure shows a siphon. The liquid shown in water. The pressure differe...
Text Solution
|
- A beaker containing a liquid is kept inside a big closed jar. If the a...
Text Solution
|
- If pressure at half the depth of a lake is equal to 2//3 pressure at t...
Text Solution
|
- A vertical U tube of uniform cross section contains mercury in both o...
Text Solution
|
- In a hydraulic press the small cylinder has a diameter of 'd1' cm, whi...
Text Solution
|
- An inverted bell lying at the bottom of a lake 47.6 m deep has 50 cm^3...
Text Solution
|
- The height to which a cylindrical vessel be filled with a homogenous l...
Text Solution
|
- A triangular lamina of area A and height h is immersed in a liquid of ...
Text Solution
|
- By sucking a straw a student can reduce the pressure in his lungs to 7...
Text Solution
|
- Two communicating vessels contain mercury. The diameter of one vessel ...
Text Solution
|
- Suppose the pressure at the surface of mercury in as barometer tube is...
Text Solution
|
- To construct a barometer, a tube of length 1m is filled completely wit...
Text Solution
|
- The vessel shown in the figure has a two sections of areas of cross-se...
Text Solution
|
- A beaker containing a liquid of density rho moves up with an accelerat...
Text Solution
|
- The pressure in a liquid at two points in the same horizontal plane ar...
Text Solution
|
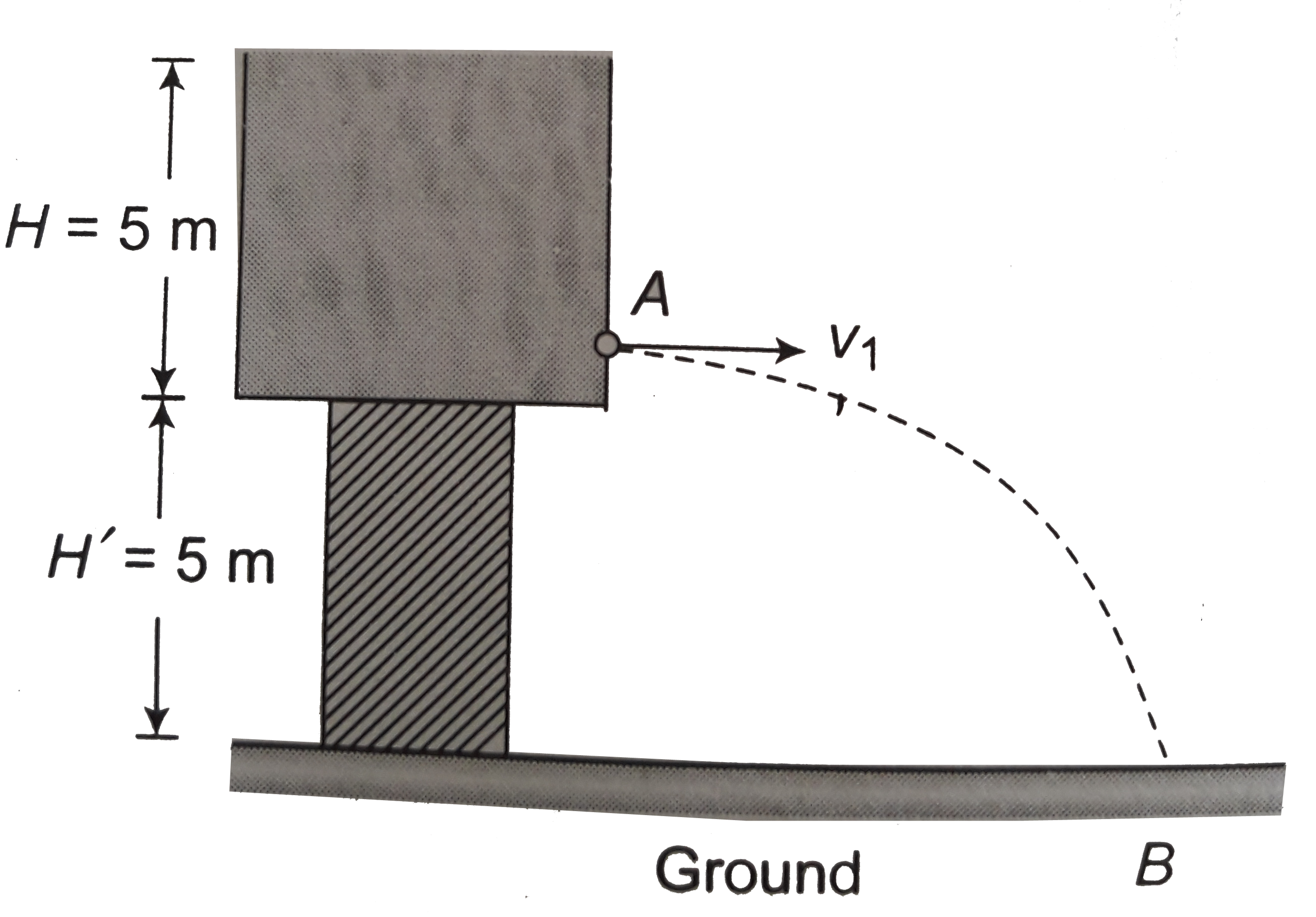
 .
.