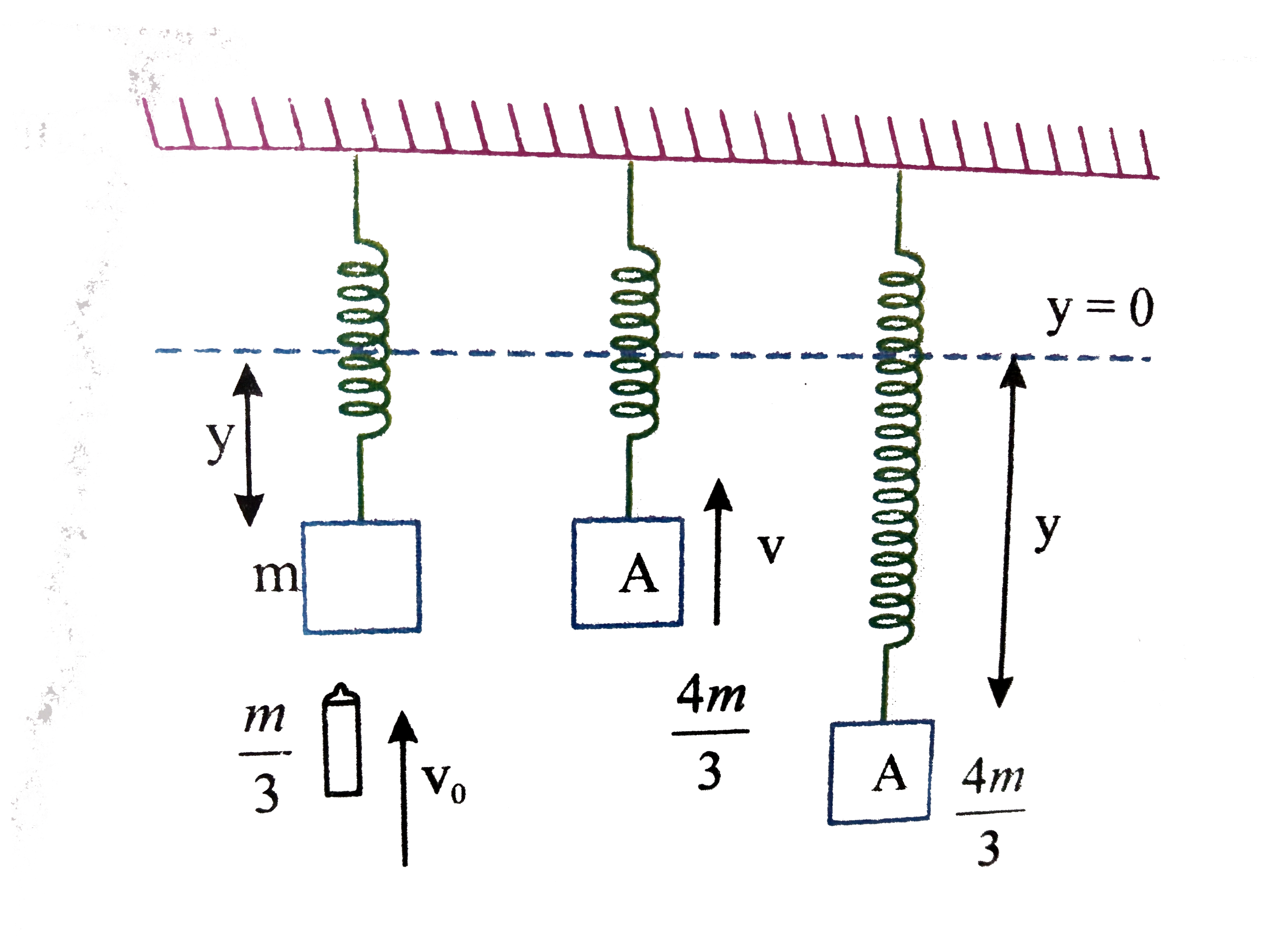
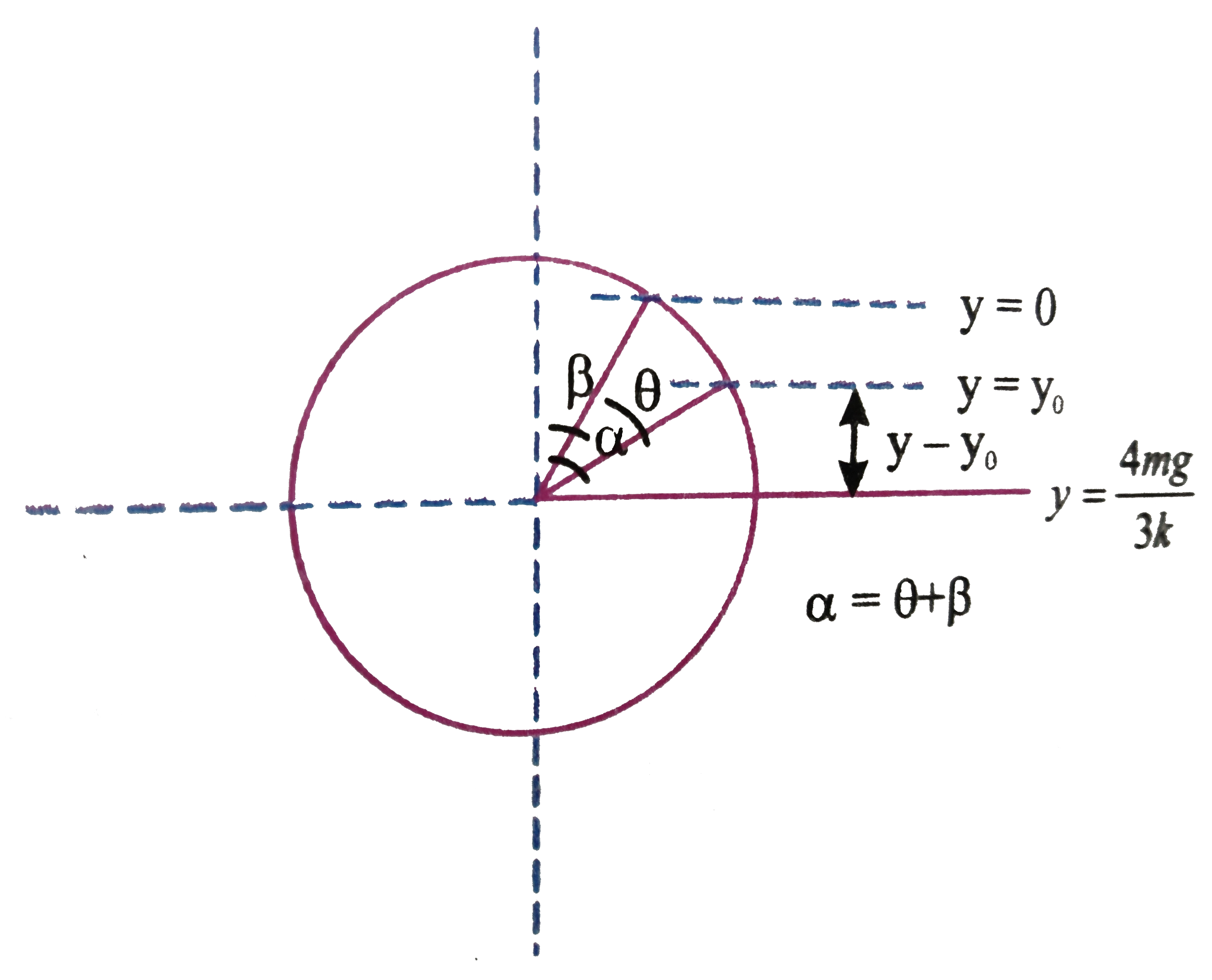
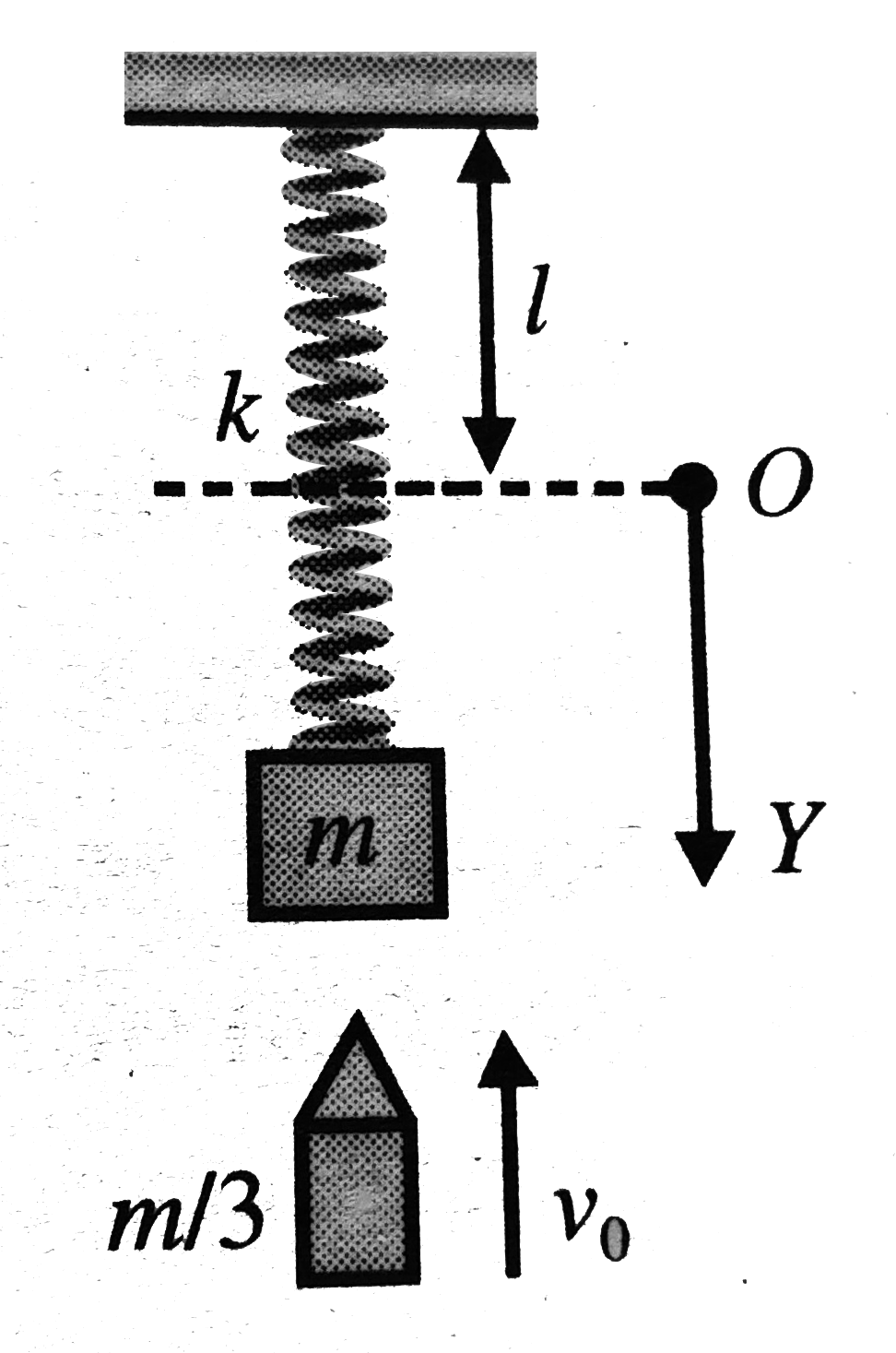A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-OSCILLATIONS-Passage
- A small block of mass m is fixed at upper end of a massive vertical sp...
Text Solution
|
- A block of mass m is suspended from one end of a light spring as shown...
Text Solution
|
- A block of mass m is suspended from one end of a light spring as shown...
Text Solution
|
- A block of mass m is connected to a spring constant k and is at rest i...
Text Solution
|
- A block of mass m is connected to a spring constant k and is at rest i...
Text Solution
|
- A plank of mass M is placed on a smooth hroizonal surface. Two light i...
Text Solution
|
- Two blocks of masses 3kg block is attached to a spring with a force co...
Text Solution
|
- Two blocks of masses 3kg block is attached to a spring with a force co...
Text Solution
|
- A cube made of wood having specific gravity 0.4 and side length a is f...
Text Solution
|
- A cube made of wood having specific gravity 0.4 and side length a is f...
Text Solution
|
- A block is attached to a spring and is placed on a horizontal smooth s...
Text Solution
|
- A block is attached to a spring and is placed on a horizontal smooth s...
Text Solution
|
- A block is tied within two spring, each having spring constant equal t...
Text Solution
|
- A block is tied within two spring, each having spring constant equal t...
Text Solution
|
- For a particle oscillating along x-axis according to equation x =A sin...
Text Solution
|
- For a particle oscillating along x-axis according to equation x =A sin...
Text Solution
|
- The distabce travelled in a time, t by a particle moving along x-axis ...
Text Solution
|
- Using graphical means find an amplitude a of oscillations resulting fr...
Text Solution
|
- A point moves in the plane y according to the law x = A sin omegat, y ...
Text Solution
|
- A point moves in the plane y according to the law x = A sin omegat, y ...
Text Solution
|