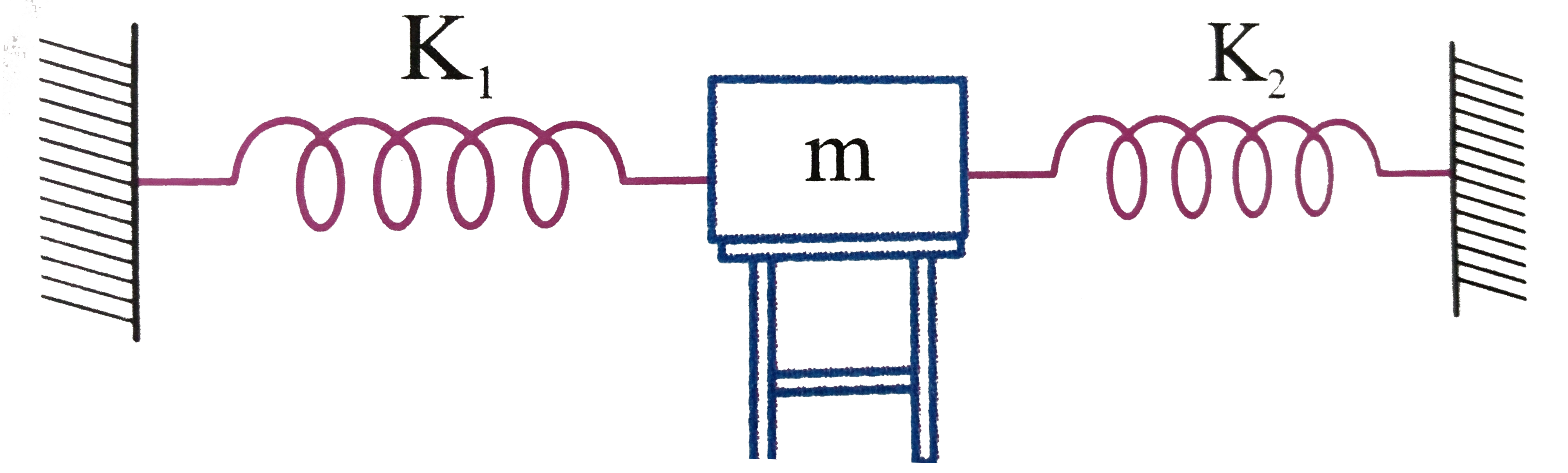
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS
NARAYNA|Exercise SIMPLE PENDULUM|14 VideosOSCILLATIONS
NARAYNA|Exercise DAMPED AND FORCED OSCILLATIONS|2 VideosOSCILLATIONS
NARAYNA|Exercise ENERGY OF A PARTICLE EXECUTING SHM|9 VideosNEWTONS LAWS OF MOTION
NARAYNA|Exercise PASSAGE TYPE QUESTION|6 VideosPHYSICAL WORLD
NARAYNA|Exercise C.U.Q|10 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-OSCILLATIONS-OSCILLATIONS DUE TO A SPRING
- A spring of force constant k is cut into two equal parts, and mass 'm'...
Text Solution
|
- A spring of natural length 80cm with a load has a length of 100cm. If ...
Text Solution
|
- In a spring block system if length of the spring is increased by 4%, t...
Text Solution
|
- An oscillating mass spring system has mechanical energy 1 joule, when ...
Text Solution
|
- Two masses (m1) and (m2) are suspended together by a massless spring o...
Text Solution
|
- A light sprial spring supports 200g weight at its lower end oscillates...
Text Solution
|
- A block of mass M is placed on a smooth table. Its two sides are attac...
Text Solution
|
- Infinite springs with force constants k, 2k, 4k, 8k,….. respectively a...
Text Solution
|
- A body of mass m is suspended from three springs as shown in figure. I...
Text Solution
|
- A load of mass M is attached to the bottom of a spring of mass 'M //3'...
Text Solution
|
- The time period of a mass loaded spring is 'T'. If 20% of its turns ar...
Text Solution
|
- Three masses 700g and 500g and 400g are suspended at the and of a spri...
Text Solution
|
- Four mass less spring whose force constant are 2k , 2k, k and 2k respe...
Text Solution
|