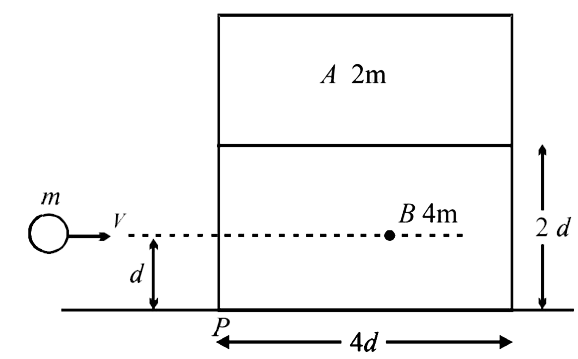
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-COLLISION-Subjective type Questions
- Two particles of mases m and m' moving on parallel straight lines are ...
Text Solution
|
- A body of mass M with a small block m placed on it rests on a smooth h...
Text Solution
|
- From a point on a smooth floor of a room a ball is shot to hit a wall...
Text Solution
|
- Stationary particles of mass m(2) is hit by another particles of mass ...
Text Solution
|
- The blocks shown in figure have equal masses. The surface of A is smoo...
Text Solution
|
- Two identical smooth balls are projected towards each other from point...
Text Solution
|
- A car P is moving with a uniform speed 5sqrt3 m//s towards a carriage ...
Text Solution
|
- An object of mass 5 kg is projecte with a velocity of 20ms^(-1) at an ...
Text Solution
|
- A block 'A' of mass 2m is placed on another block 'B' of mass 4m which...
Text Solution
|