A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-WORK POWER AND ENERGY-Level-VI (Multiple Answer)
- The potential energy of a particle moving along x-axis is given by U =...
Text Solution
|
- A block of mass 1 kg moves towards a spring of force constant 10 N//m....
Text Solution
|
- The spring constant of spring A is twice the spring constant of spring...
Text Solution
|
- A particle of mass 1 kg is moving X-axis. Its velocity is 6 m//s at x ...
Text Solution
|
- A particle sides down from rest on an inclined plane of angle theta wi...
Text Solution
|
- A particle is taken from point A to point B under the influence of a f...
Text Solution
|
- An engine is pulling a train of mass m on a level track at a uniform s...
Text Solution
|
- The alternative that gives the conservative force of the following is.
Text Solution
|
- A man is standing on a plank which is placed on smooth horizontal surf...
Text Solution
|
- A small sphere of mass m suspended by a thread is first taken a side s...
Text Solution
|
- A particle P is initially at rest on the top pfa smooth hemispherical ...
Text Solution
|
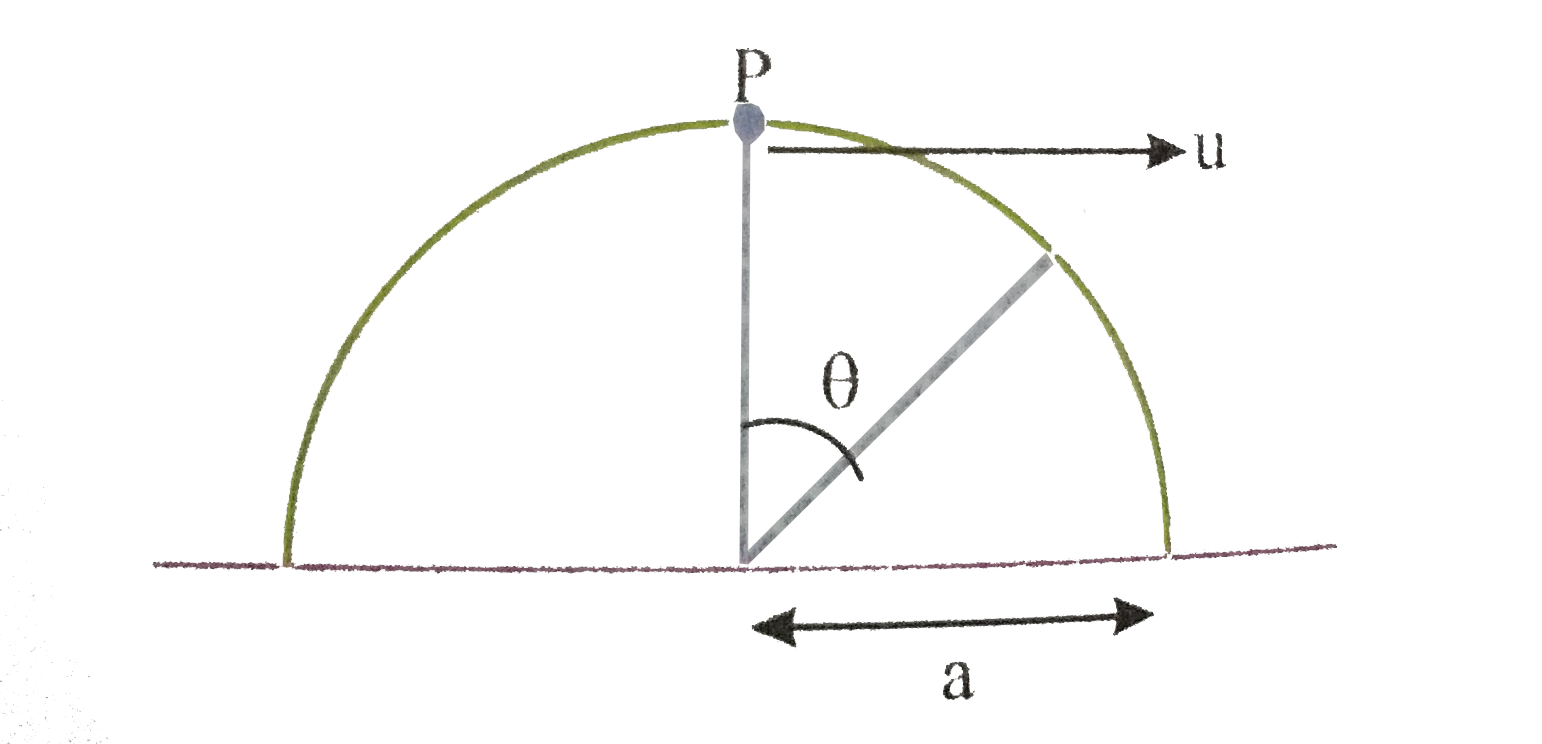 .
.