Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-WORK POWER AND ENERGY-Level-VI (Integer)
- A ball leaves the track at B which is at 3m height from bottom most po...
Text Solution
|
- The displacement x (in m), of a patticle of mass m (in kg) is related ...
Text Solution
|
- Block A of mass 1 kg is placed on the rough surface of block B of mass...
Text Solution
|
- A block of mass 2 kg is placed on an inclined plane of angle 53^@, att...
Text Solution
|
- Figure shows a light, inextensible string attached to a cart that can ...
Text Solution
|
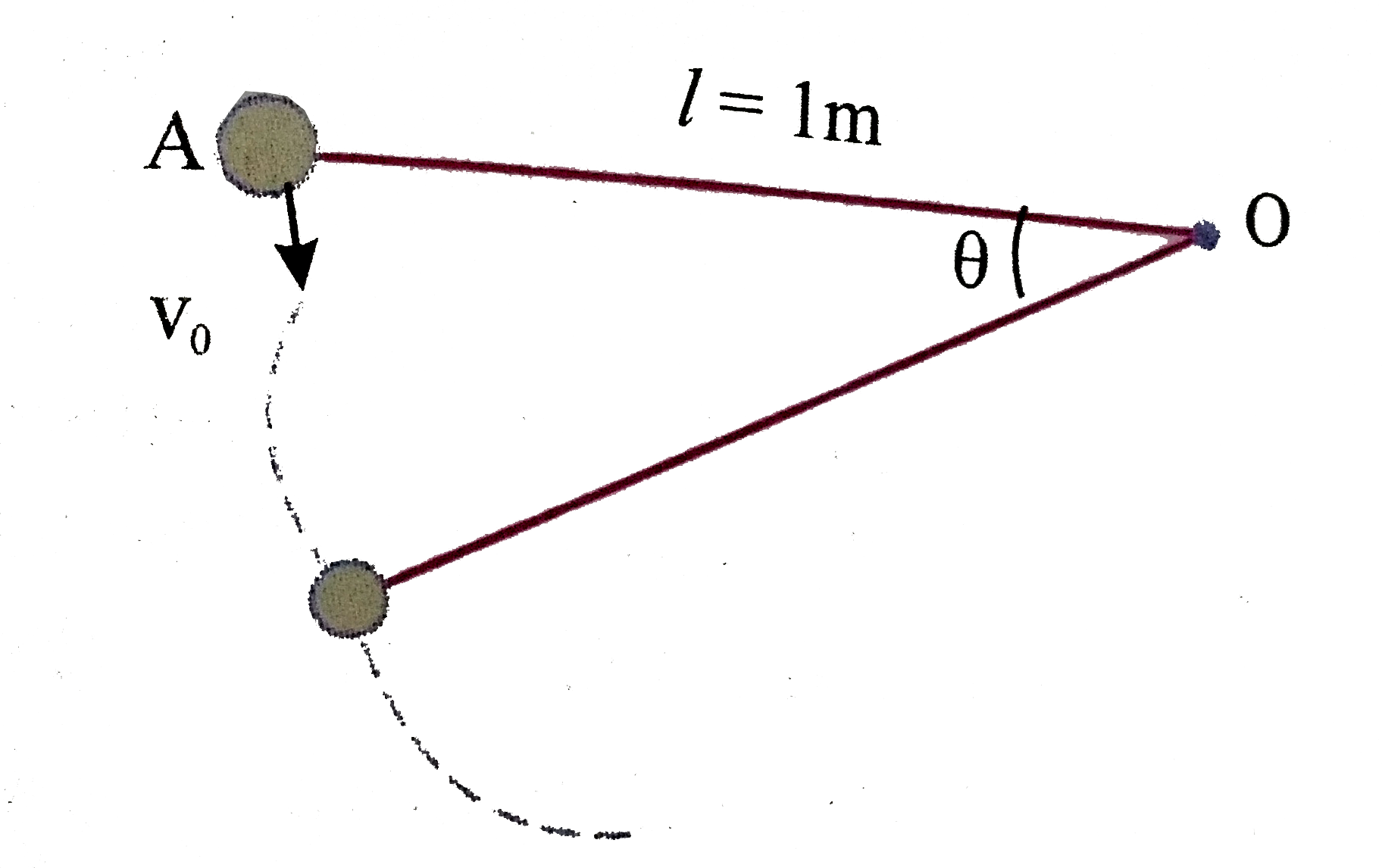
- A particle is suspended vertically from a point O by an inextensible m...
Text Solution
|
- The sphere at P is given a down ward velocity v(0) and swings in a ver...
Text Solution
|
- A block of mass 0.18 kg is attached to a spring of force-constant 2 N/...
Text Solution
|
- A particle of mass 0.2 kg is moving in one dimension under a force tha...
Text Solution
|
- An observed and a vehicle, both starts moving together from rest with ...
Text Solution
|
- Two block A and B are placed one over other. Blocks B is acted upon by...
Text Solution
|
- A block of mass m is placed inside a smooth hollow cylinder of radius ...
Text Solution
|
 .
.