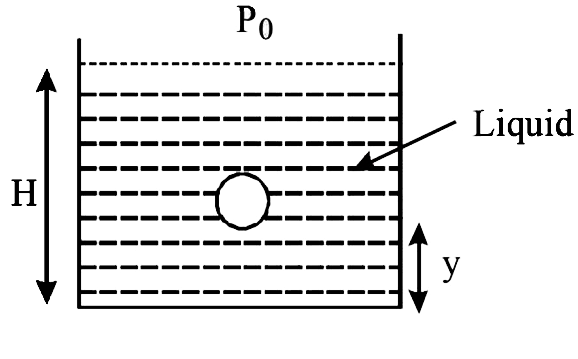
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-KINETIC THEORY OF GASES-LEVEL-VI
- A vessel of volume V(0) contains an ideal gas at pressure p(0) and tem...
Text Solution
|
- Assume that the temperature remains essentially constant in the upper ...
Text Solution
|
- Assume a sample of a gas in a vessel. The speeds of molecules are betw...
Text Solution
|
- Tyre of a bicycle has voulme 2xx10^(-3)m^(3) Initially the tube is fil...
Text Solution
|
- A small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped ...
Text Solution
|
- A small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped ...
Text Solution
|
- A small spherical monoatomic ideal gas bubble (gamma=5//3) is trapped ...
Text Solution
|
- A very tall vertical cylinder is filled with a gas of molar mass M und...
Text Solution
|
- A very tall vertical cylinder is filled with a gas of molar mass M und...
Text Solution
|
- A very tall vertical cylinder is filled with a gas of molar mass M und...
Text Solution
|