A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FIITJEE-TEST PAPERS-PHYSICS
- A sphere of mass m and radius r rolls without slipping over a tunnel o...
Text Solution
|
- In the given figure, a long platform of mass m is placed on frictionle...
Text Solution
|
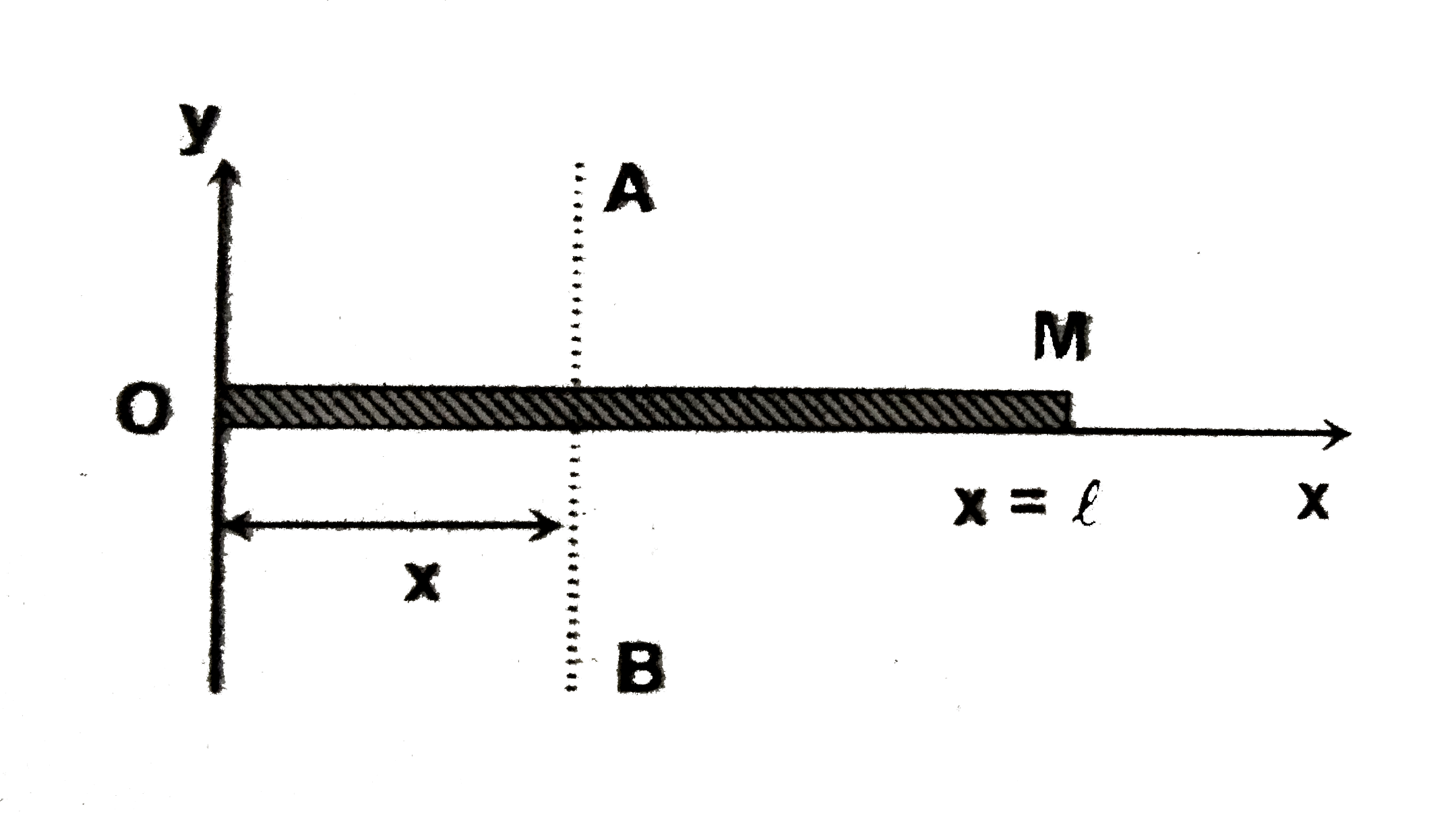
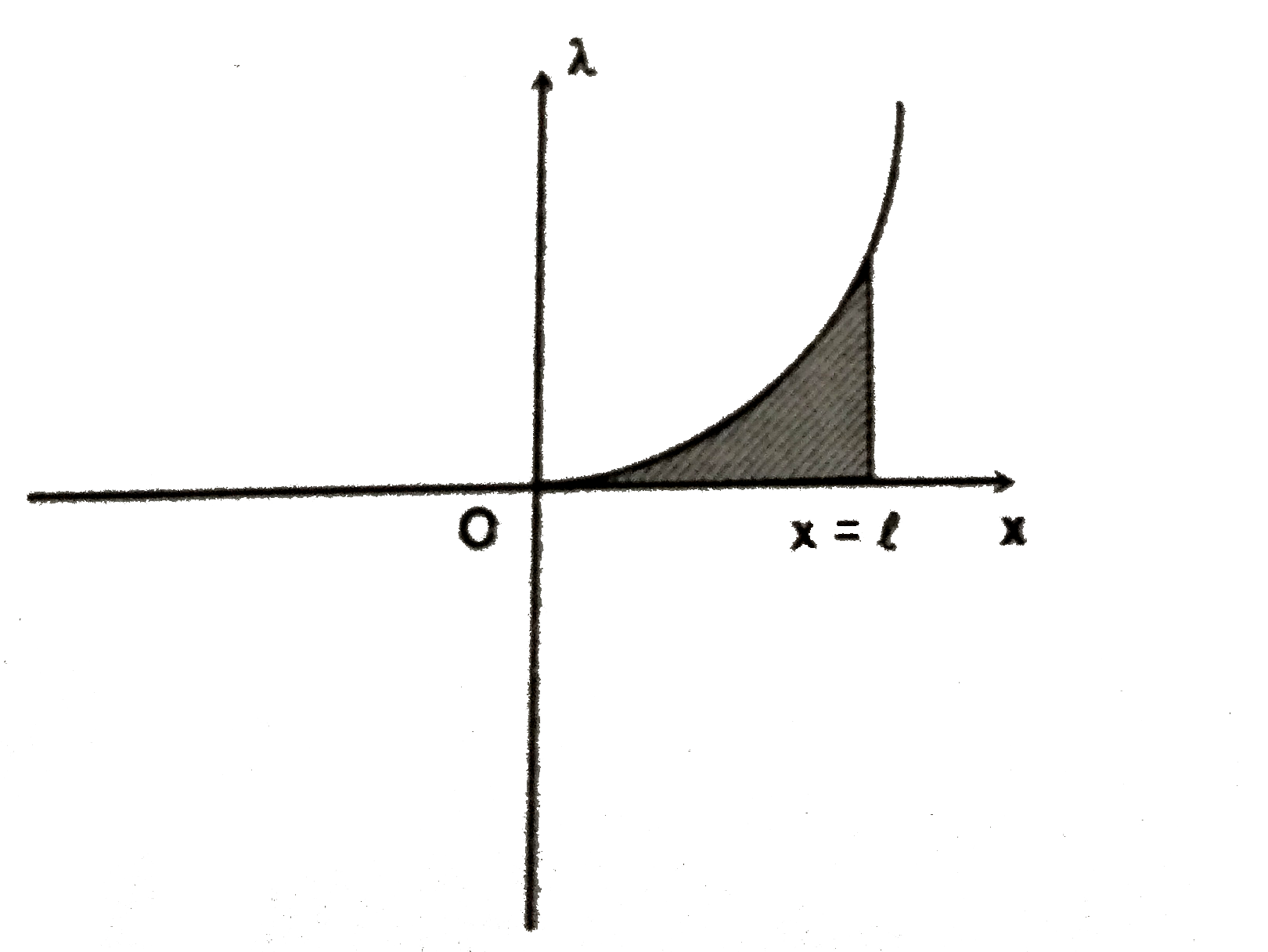
- A non uniform rod OM (of length l m) is kept along x-axis and rotating...
Text Solution
|
- Identical constant forces push two identical cars A and B continuously...
Text Solution
|
- Two moles of an ideal monoatomic gas is taken through a cyclic process...
Text Solution
|
- Two ends of a rod of uniform cross sectional area are kept at temperat...
Text Solution
|
- An ideal gas is taken through a process PT^(3)= constant. The coeffici...
Text Solution
|
- 4 kg of ice at -20^(@)C is mixed with 5 kg of water at 40^(@)C. The wa...
Text Solution
|
- The molar heat capacity of an ideal gas in a process varies as C=C(V)+...
Text Solution
|
- A point charge q'q is placed at distance 'a' from the centre of an unc...
Text Solution
|
- A solid sphere of radius 'R' density rho and specific heat 'S' initial...
Text Solution
|
- Two point electric dipoles with dipole moment P(1) and P(2) are separa...
Text Solution
|
- 4 moles of an ideal monoatomic gas is heated isobarically so that its ...
Text Solution
|
- A point charge 'q' is placed at the centre of left circular end of a c...
Text Solution
|
- Two concentric spherical conducting shells of radii 'a' and 2a are ini...
Text Solution
|
- Three capacitors of capacitances 5muF,2muF and 2muF are charged to 20 ...
Text Solution
|
- Three concentric spherical conducting shells A, B and C of radii a, 2a...
Text Solution
|
- In the circuit shown the cell will deliver maximum power to the networ...
Text Solution
|
- In the circuit shown, all the capacitors are initially uncharged. The ...
Text Solution
|
- A particle of charge 'q' and mass 'm' enters a uniform magnetic field ...
Text Solution
|