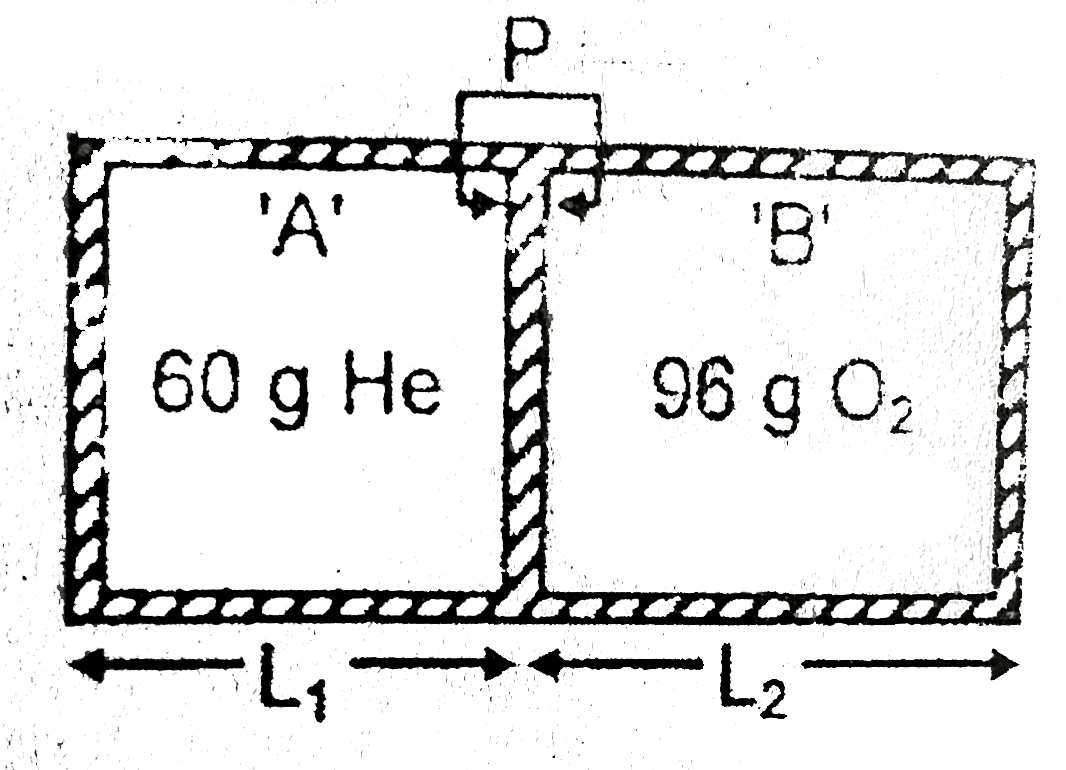
A cylindrical diathemic chamber fitted with movable, massless & frictionless piston. Initially piston was at rest by the stop pin `P` as shown in figure. Compartment `(A)` is filled with `60g` He gas & compartment `(B)` is filled with `96 g of O_(2)` gas ast `27^(@)C` . Assume ideal behaviour of gas, then calculate ratio `(L_(1))/(L_(2))` , if stop pin is suddenly removed ? \
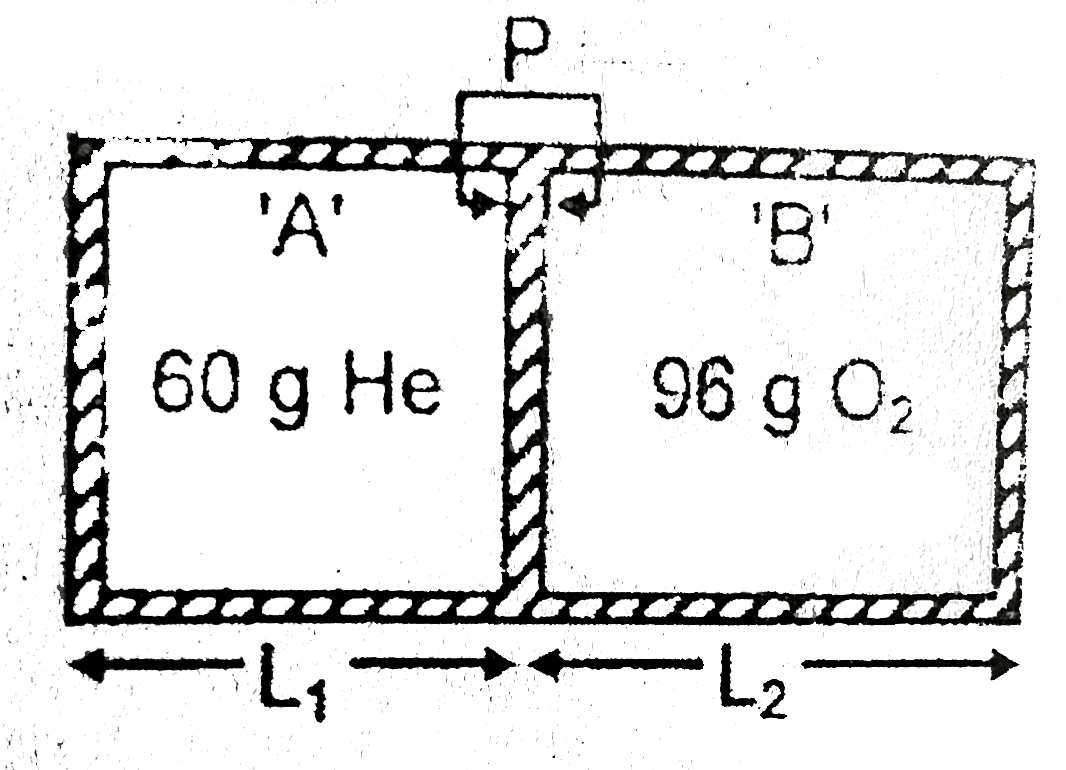
A cylindrical diathemic chamber fitted with movable, massless & frictionless piston. Initially piston was at rest by the stop pin `P` as shown in figure. Compartment `(A)` is filled with `60g` He gas & compartment `(B)` is filled with `96 g of O_(2)` gas ast `27^(@)C` . Assume ideal behaviour of gas, then calculate ratio `(L_(1))/(L_(2))` , if stop pin is suddenly removed ? \
A
`2`
B
`4`
C
`5`
D
`6`
Text Solution
Verified by Experts
The correct Answer is:
C

At equilibrium, `F_(He) = F_(O_(2))`
`n_(He)(RT)/(V_(He))xx A = (n_(O_(2))RTxxA)/(VO_(2))`
`(n_(He))/(L_(1)) = (n_(O_(2)))/(L_(2))`
`:. (L_(1))/(L_(2)) = (n_(He))/(n_(O_(2))) = (60//4)/(96//32) = (15)/(3) = 5`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
In the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatmoic gas at 400K. The heat capacities per mole of an ideal monatomic gas are C_V=3/2R, C_P=5/2R, and those for an ideal diatomic gas are C_V=5/2R, C_P=7/2R, Now consider the partition to be free to move without friction so that the pressure of gasses in both compartments is the same. The total work done by the gases till the time they achives equilibrium will be
In Fig., a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. the lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. the heat capacities per mole of an ideal monoatomic gas are C_(upsilon) = (3)/(2) R and C_(P) = (5)/(2) R , and those for an ideal diatomic gas are C_(upsilone) = (5)/(2) R and C_(P) = (7)/(2) R. Now consider the partition to be free to move without friction so that the pressure of gases in both compartments is the same. the total work done by the gases till the time they achieve equilibrium will be
A cylindrical tube ofuniform cross sectional area A is fitted with two frictionless pistons, as shown in figure-2.46. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is equal to atmospheric pressure P_0 and temperature is T^0 . If the temperature of the gas is increased to 2T_0 , find the tension in the wire.
In the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatmoic gas at 400K. The heat capacities per mole of an ideal monatomic gas are C_V=3/2R, C_P=5/2R, and those for an ideal diatomic gas are C_V=5/2R, C_P=7/2R, Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be
In Fig., a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulating material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. the lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700 K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400 K. the heat capacities per mole of an ideal monoatomic gas are C_(upsilon) = (3)/(2) R and C_(P) = (5)/(2) R , and those for an ideal diatomic gas are C_(upsilone) = (5)/(2) R and C_(P) = (7)/(2) R. Consider the partition to be rigidly fixed so that it does not move. when equilibrium is achieved, the final temperature of the gases will be
A mixture of ethane (C_(2)H_(6)) and ethene (C_(2)H_(4)) occupies 40 L at 1.00 atm and at 400 K . The mixture reacts completely with 130 g of O_(2) to produce CO_(2) and H_(2)O . Assuming ideal gas behaviour, calculate the mole fractions of C_(2)H_(4) and C_(2)H_(6) in the mixture.
A diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m^2 . Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.