Text Solution
Verified by Experts
Topper's Solved these Questions
LAWS OF MOTION
AAKASH INSTITUTE|Exercise TRY YOURSELF|67 VideosLAWS OF MOTION
AAKASH INSTITUTE|Exercise ASSIGNMENT ( SECTION -A)|48 VideosLAWS OF MOTION
AAKASH INSTITUTE|Exercise Assignment (SECTION-D) (Assertion-Reason Type Questions)|15 VideosKINETIC THEORY
AAKASH INSTITUTE|Exercise EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions|10 VideosMAGNETISM AND MATTER
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION D)|26 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-LAWS OF MOTION-Illustration
- Consider an object of mass m moving in free space with velocity given ...
Text Solution
|
- A variable force acts on a body of mass 2 kg initially at rest as show...
Text Solution
|
- A two block system is shown in figure . We shall draw complete free bo...
Text Solution
|
- When two block of masses m(1) and m(2) are connected by a massless str...
Text Solution
|
- Two block of masses m(1) and m(2) are lying on a frictionless horizont...
Text Solution
|
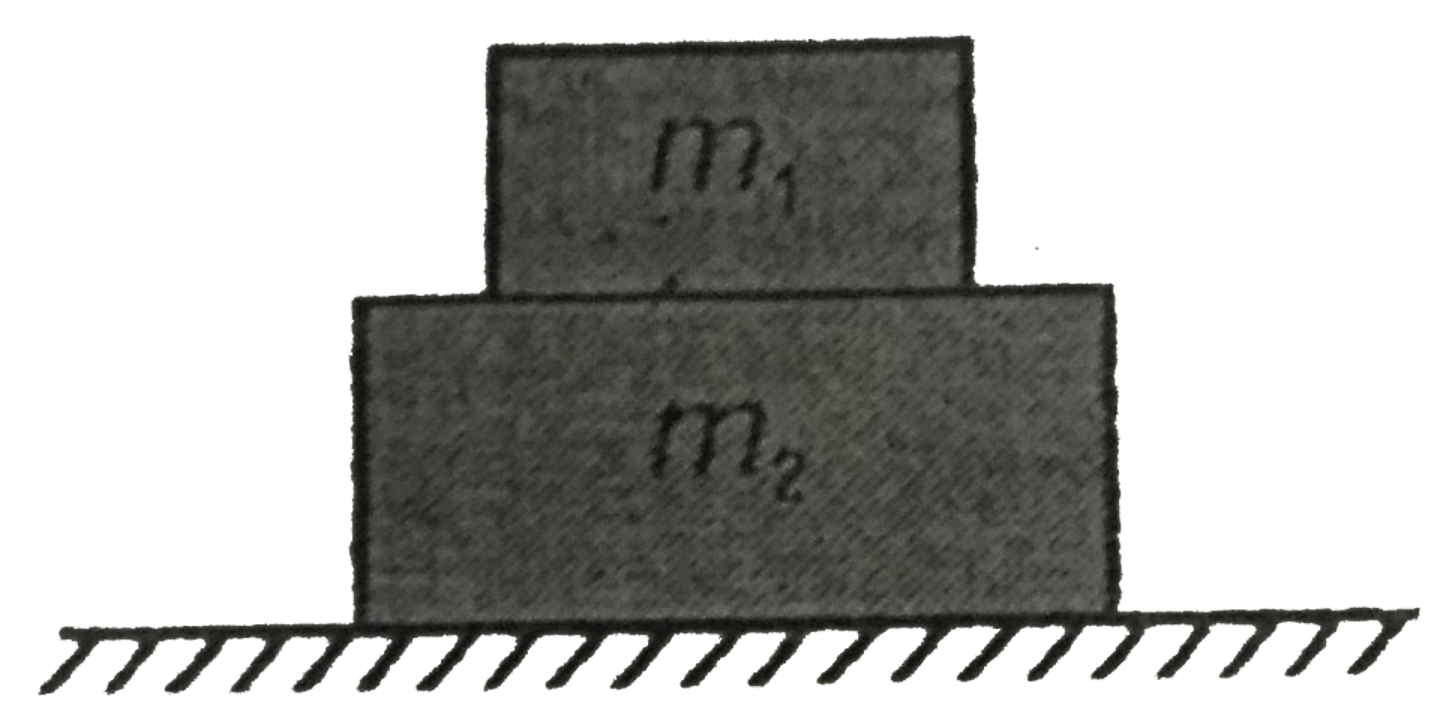
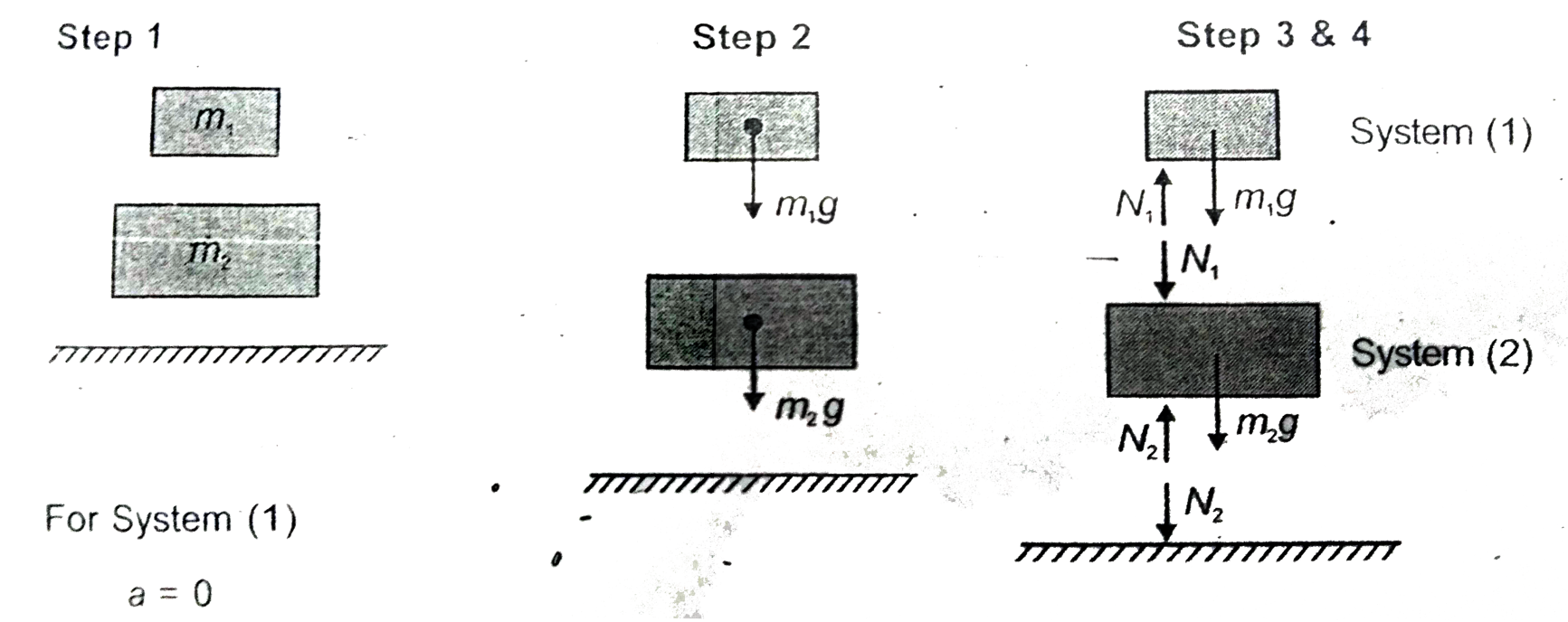 For system (1)
For system (1)