Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 26|8 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 27|3 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise TRUE/FALSE|2 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 25
- Two blocks A and B each of mass m are placed on a smooth horizontal su...
Text Solution
|
- In the figure shown, a person wants to raise a block lying on the grou...
Text Solution
|
- In pulley syste shown in figure, block C is going up at 2(m)/(s) and b...
Text Solution
|
- Two blocks A and B of masses m and 2m, respectively , are held at rest...
Text Solution
|
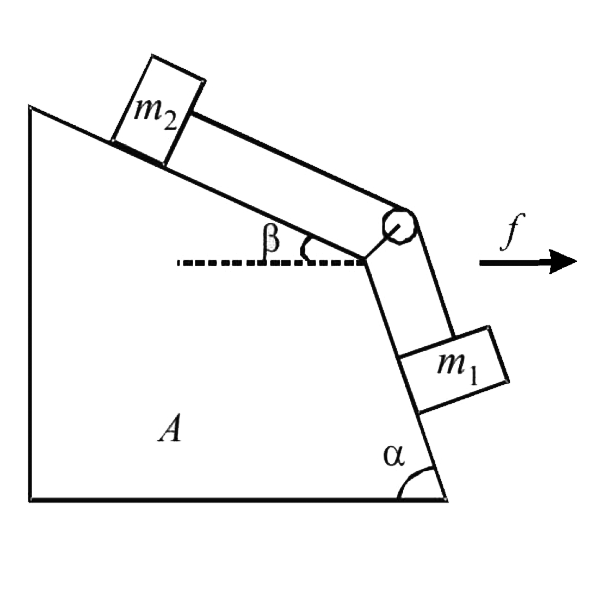
- Two cubes of masses m1 and m2 be on two frictionless slopes of block A...
Text Solution
|