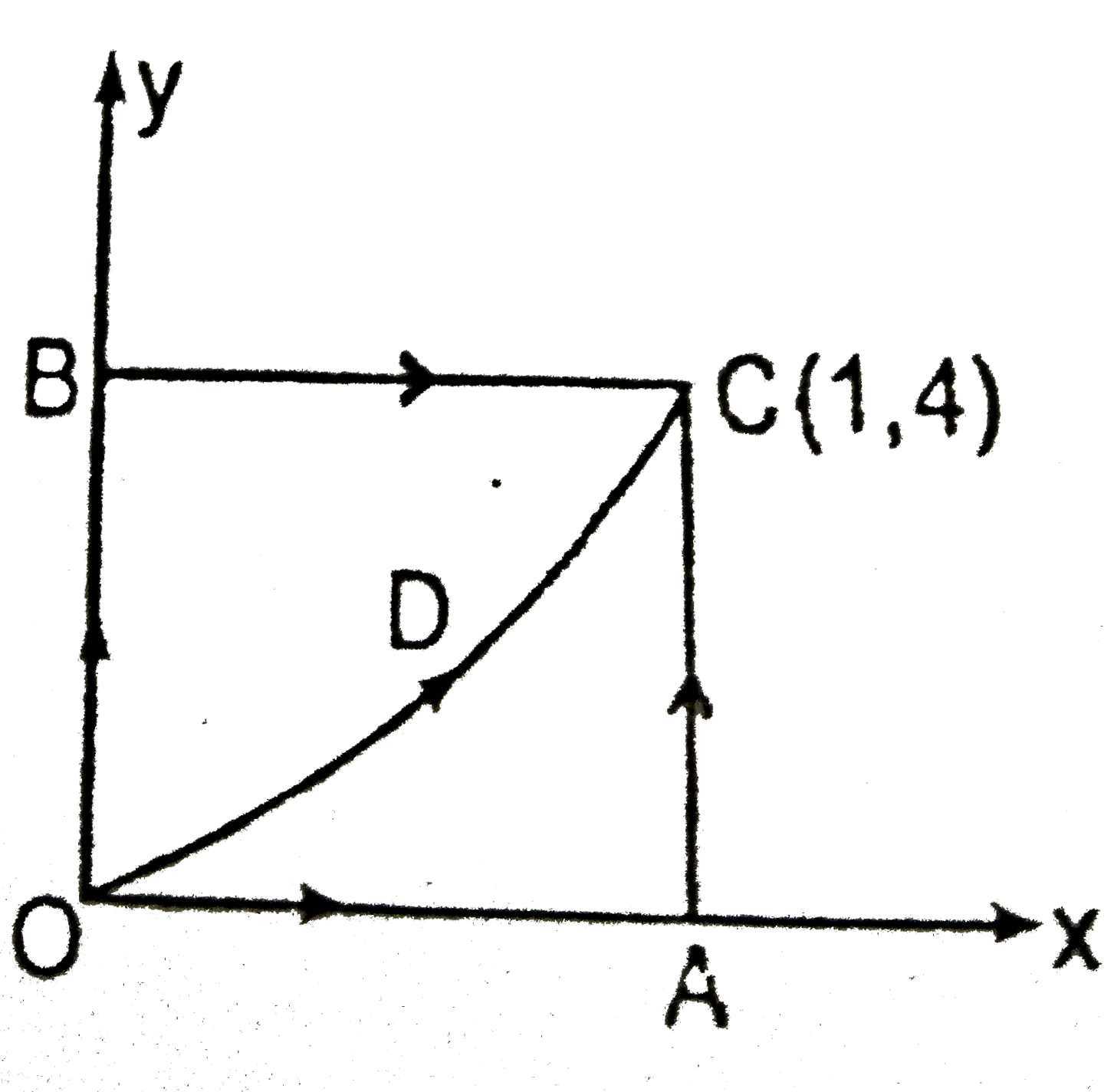Home
Class 11
PHYSICS
A particle is moved along the different ...

A particle is moved along the different paths `OAC, OBC & ODC` as shown in the figure . Path `ODC` is a parabola , `y=4x^(2)`. Find the work done by a forc `vec(F)=xyhat(i)+x^(2)y` on the particle along these paths. Is this force a conservative force ?

Text Solution

Verified by Experts

The correct Answer is:
`w_(OAC)=8J,w_(OBC)=2J;w_(ODC)=19//3j,No`
`(W_(F))_(OAC)=int (xydx+x^(2)ydy)`
`=underset(0)overset(A)int (xydx=x^(2)ydy)+underset(A)overset(C)int(xydx+s^(2)ydy)`
ON `OA` path `,`
`y=0,dy=0` and on `AC` path
`x=1.dx=0`
`(W_(F))_(OAC)=underset(0)overset(A)int (0.dx+0.dy)+underset(y=0)overset(y=4)int(0+1ydy)=8J`
`(W_(F))_(OAC)=0+underset(B)overset(C)int(xy dx+x^(2)ydy)`
`=underset(x=0)overset(1)int {x4x+x^(2)4(0)}=2J`
`=underset(0)overset(1)int (x4x^(2)dx+x^(2)4x^(2)8xdx)=1+(32)/(6)=(19)/(3)J`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 40|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 41|7 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 38|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A particle is moved foom the orgin A, back to the origin, along the path ABCDEFA as shown in figure (A) Find the work done by the force vecF=y hati+zhatj+xhatk acting on the particle, in the round trip? (B) Is the force given in part (A) conservative?

The work done by a force vec(F)=(-6x^(3)hat(i)) N in displacing a particle from x = 4m to x = - 2m is

A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

Shown that work done by a conservative force on a particle moving between two points is path independent.

Calculate the work done by the force vec(F) = y hat(i) to move the particle from (0,0) to (1,1) in the following condition (a) y = x (b) y = x^(2)

The work done by the force vec(F)=A(y^(2) hati+2x^(2)hatj) , where A is a constant and x & y are in meters around the path shown is :

A particle is moving with a constant speed along a straight line path. A force is not required to

A particle moves along the parabolic path y=ax^(2) in such a The accleration of the particle is:

A force F is related to the position of a particle by the relation F=(10x^(2))N . Find the work done by the force when the particle moves from x=2m to x=4m .

A particle has initial velocity vec(v)=3hat(i)+4hat(j) and a constant force vec(F)=4hat(i)-3hat(j) acts on the particle. The path of the particle is :