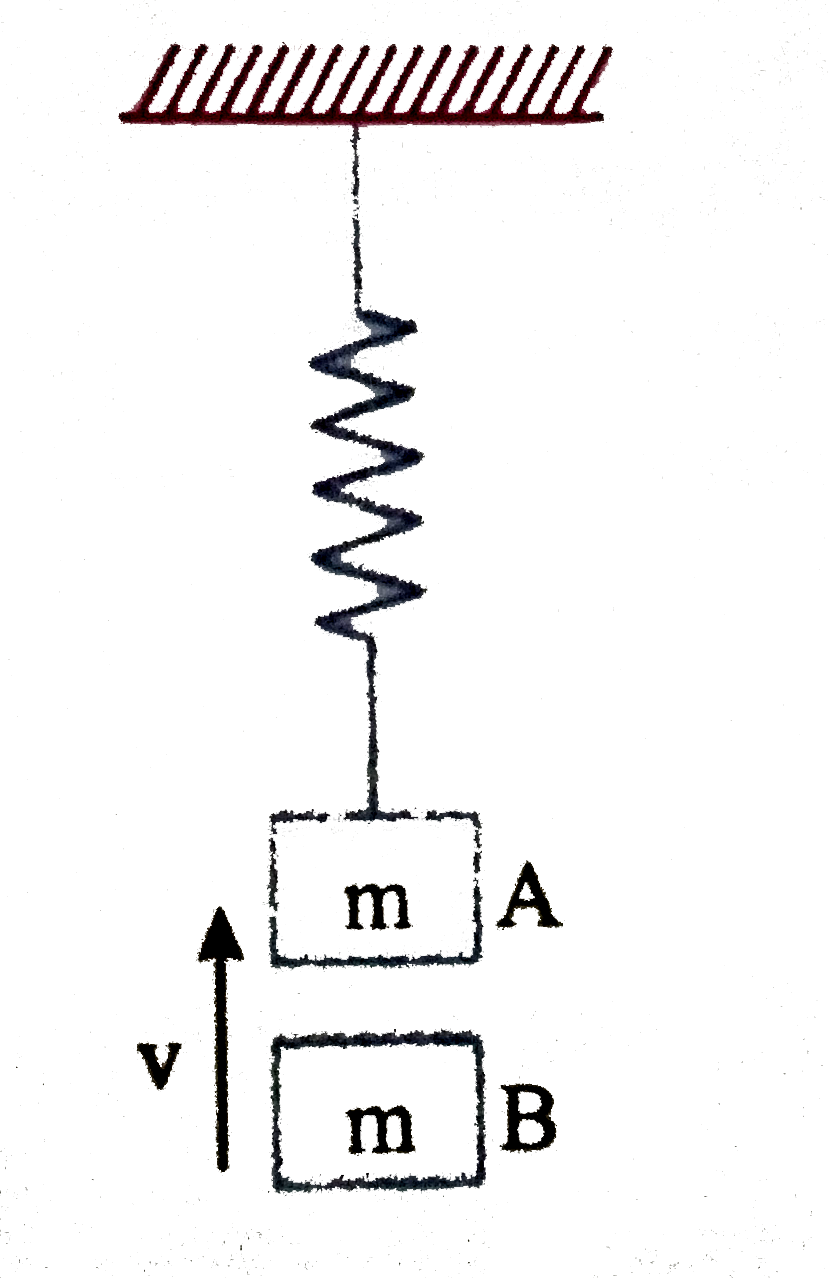A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 57|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 58|9 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP 55|8 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 56
- A stone of mass M is tied at the end of a string, is moving in a circl...
Text Solution
|
- A hollow sphere of mass 'm' and radius R rests on a smooth horizontal ...
Text Solution
|
- In the figure shown a cart moves on a smooth horizontal surface due to...
Text Solution
|
- Block A is hanging from vertical spring of spring constant K and is re...
Text Solution
|
- A strip of wood mass M and length l is placed on a smooth horizontal s...
Text Solution
|
- Initial velocity and acceleration of a particles are as shown in the ...
Text Solution
|
- Statement I: If a sphere of mass mmoving with speed u undergoes a perf...
Text Solution
|