Home
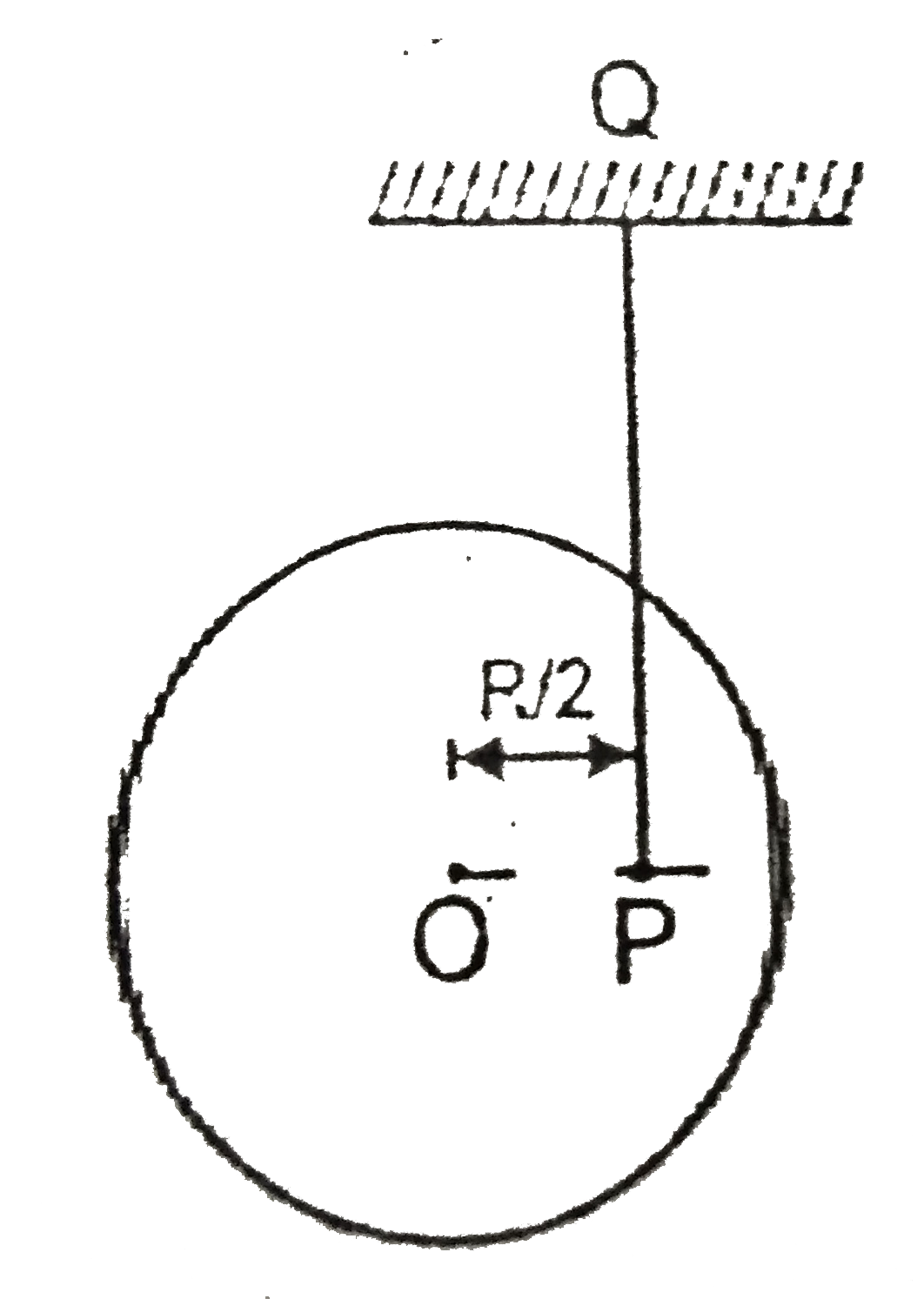
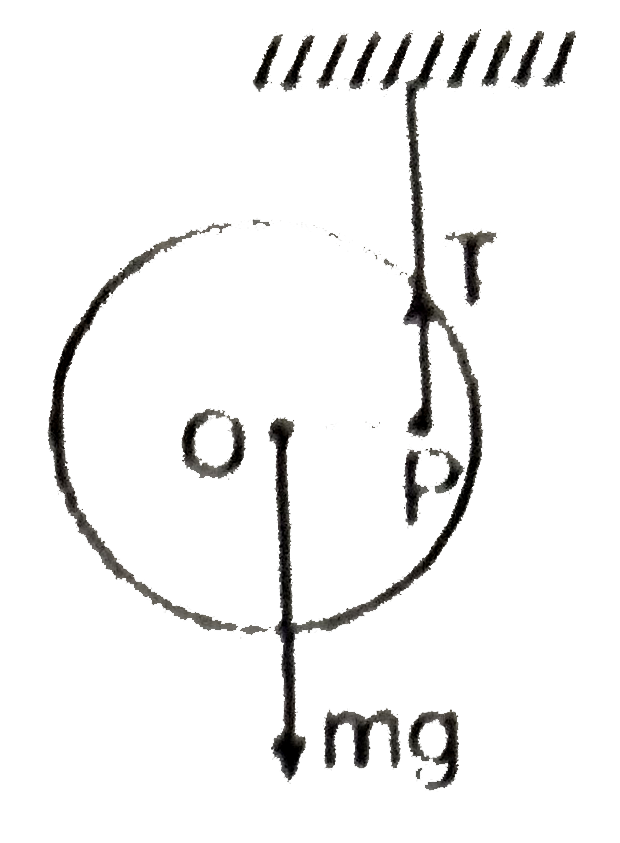
Class 11
PHYSICS
A uniform disc of mass M and radius R is...

A uniform disc of mass `M` and radius `R` is released from the shown position . `PQ` is s tring , `OP` is a horizontal line , `O` is the centre of the disc and distance `OP` is `R//2`. The tension in the string just after the disc is released will be `:`

A

`(Mg)/(2)`

B

`(Mg)/(3)`

C

`(2Mg)/(3)`

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
C
`(C )`
Applying Newton's law on the centre of mass `O`
`Mg-T=ma {a=` acceleration of centre of mass `}`
`tau = I alpha`, about centre of mass
`T=(R)/(2)=(MR^(2))/(2).alpha`
Also `a=(R)/(2)alpha` from above equations `T=(2mg)/(3)`
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 66|4 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 67|2 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 64|5 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is

A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information Reaction force exerted by the hinge on the disc at this instant is

A disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information The angular velocity of the disc in the above described case is

Given a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs

A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.

A semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of (4R)/(3pi) from the point O . Now the disc is released from this position so that it starts rolling without slipping. Find (a) The angular acceleration of the disc at the moment it is relased from the given position. (b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.