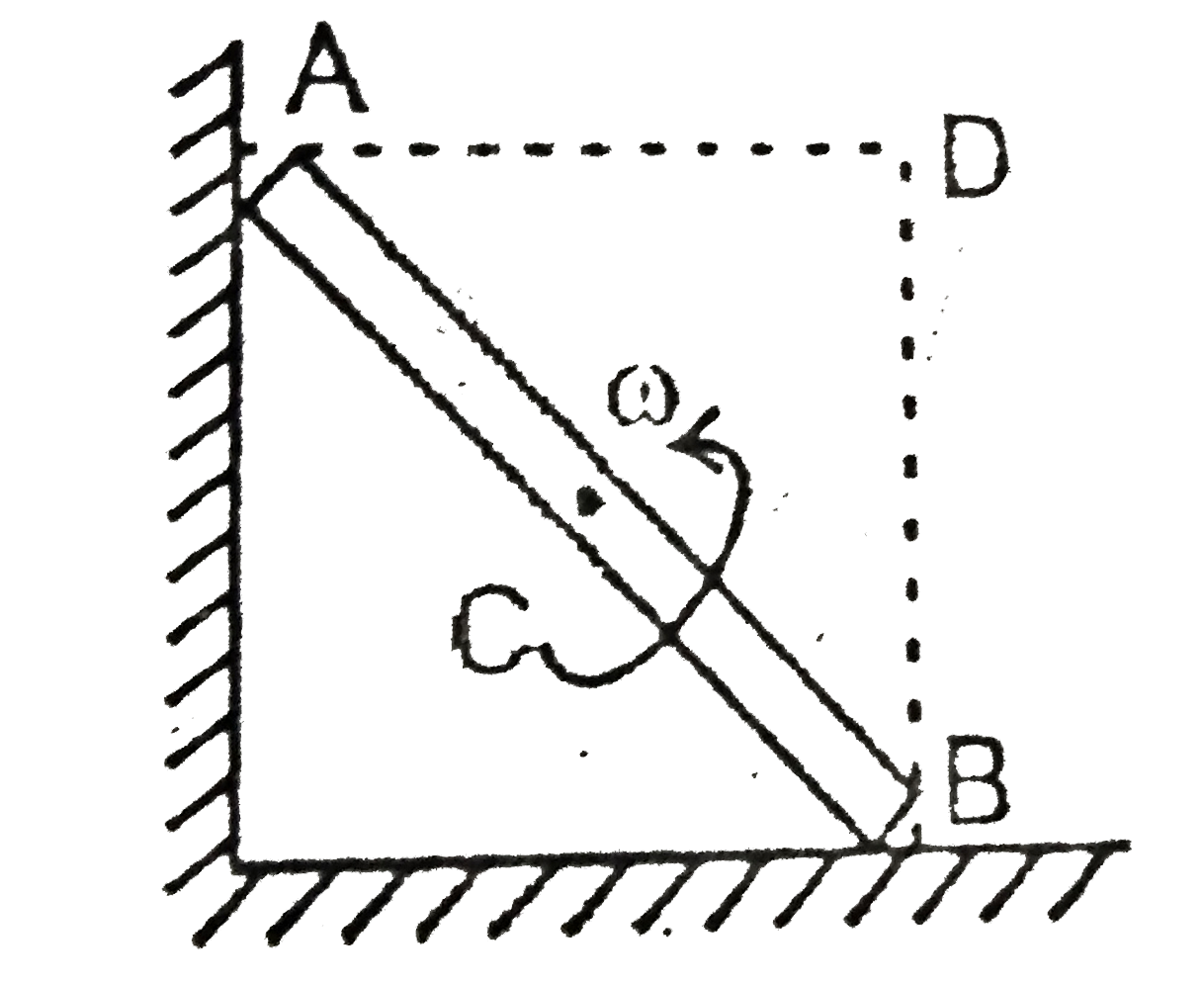
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 67|2 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 68|7 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise DPP 65|5 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 66
- A ring and a disc of same mass m and same radius R are joinged concent...
Text Solution
|
- A particle of mass m is moving along the x-axis with speed v when It c...
Text Solution
|
- A thin uniform rod AB is sliding between two fixed right angled surfac...
Text Solution
|
- A solid sphere of mass m and radiusr is given an initial angular veloc...
Text Solution
|