A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
DAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 75|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp 76|5 VideosDAILY PRACTICE PROBLEMS
RESONANCE|Exercise dpp73|4 VideosCURRENT ELECTRICITY
RESONANCE|Exercise Exercise|54 VideosELASTICITY AND VISCOCITY
RESONANCE|Exercise Advanced Level Problems|9 Videos
Similar Questions
Explore conceptually related problems
RESONANCE-DAILY PRACTICE PROBLEMS-dpp 74
- A man stands on a weighing machine kept inside a lift. Initially the l...
Text Solution
|
- A horizontal spring -block system of mass 2kg executes S.H.M when the ...
Text Solution
|
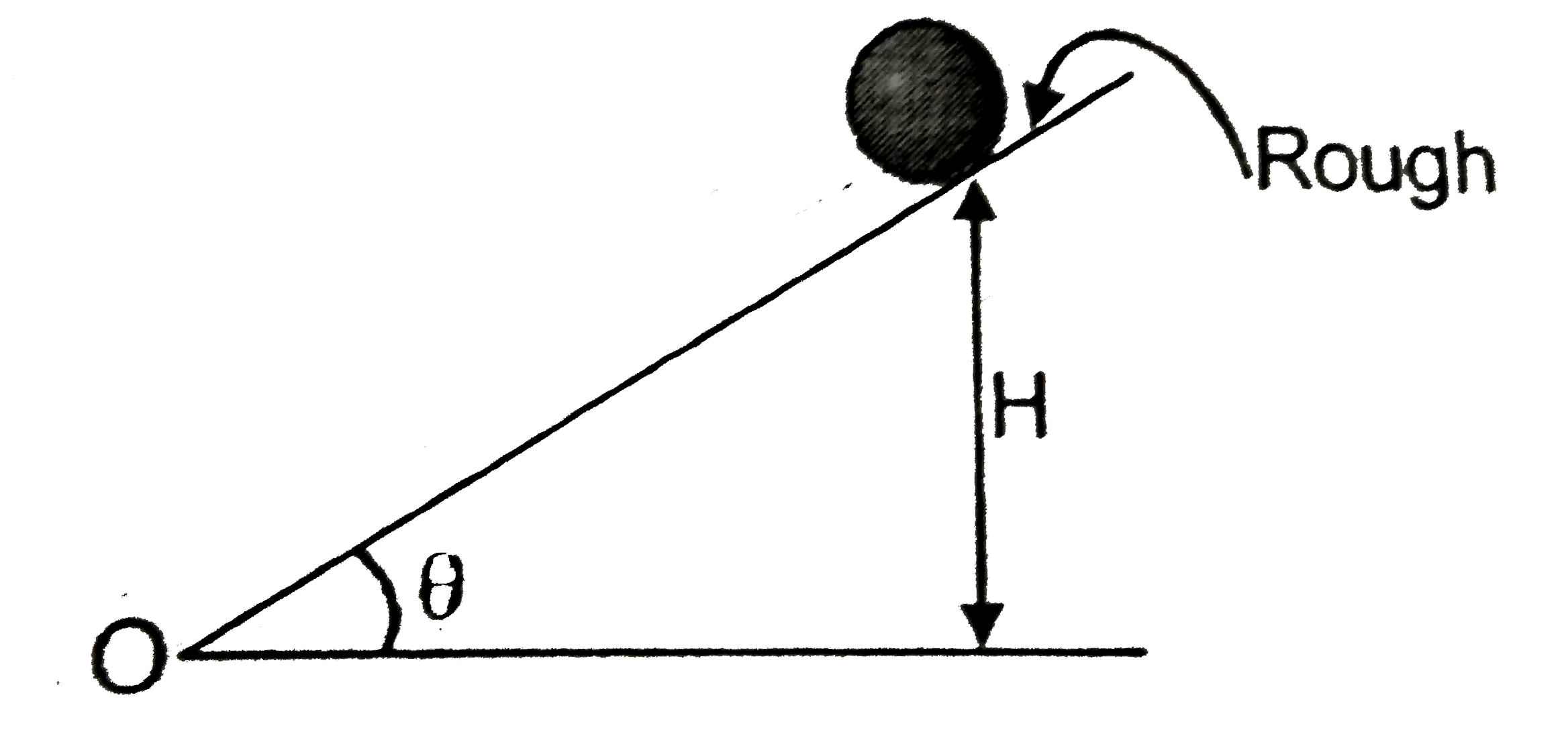
- A solid ball of mass 'm' is released on a rough fixed inclined plane f...
Text Solution
|
- A particle of mass 1kg moves from rest along a straight line due to ac...
Text Solution
|
- A particle is projected from ground with an initial velocity 20m//sec ...
Text Solution
|
- A block of mass m(1)=1kg is attached to a spring of force constant k=2...
Text Solution
|
- A mass M is in static equilibrium on a massless vertical spring as sho...
Text Solution
|