Home
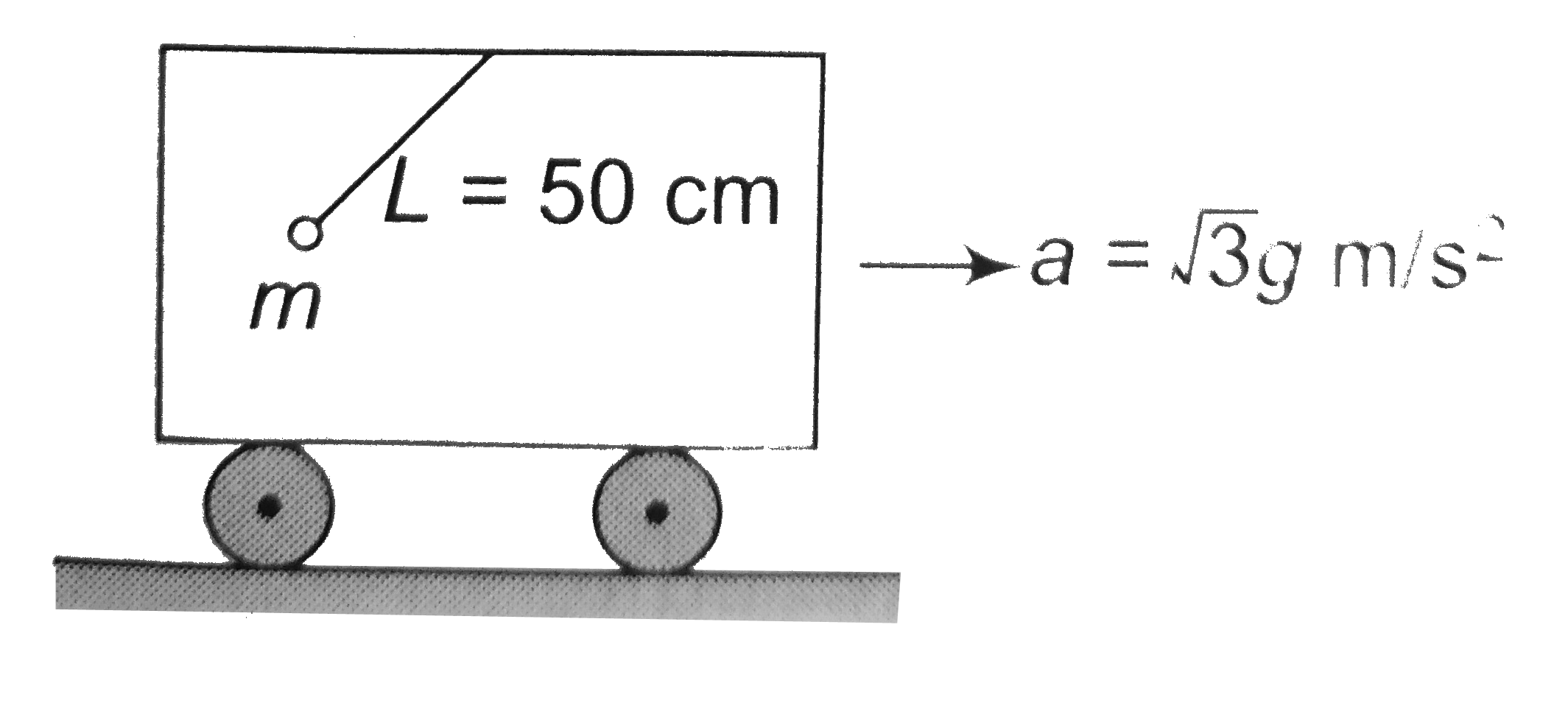
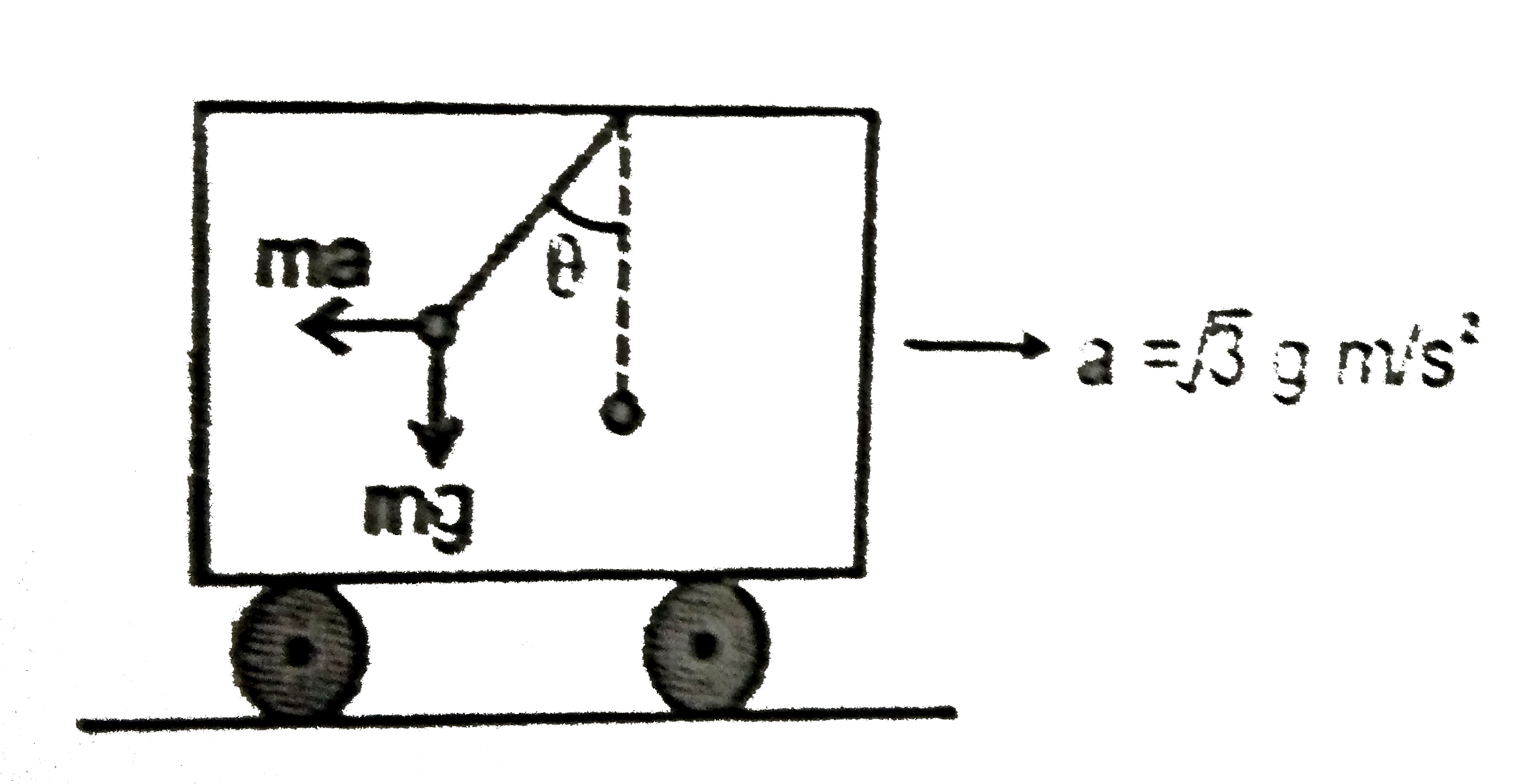
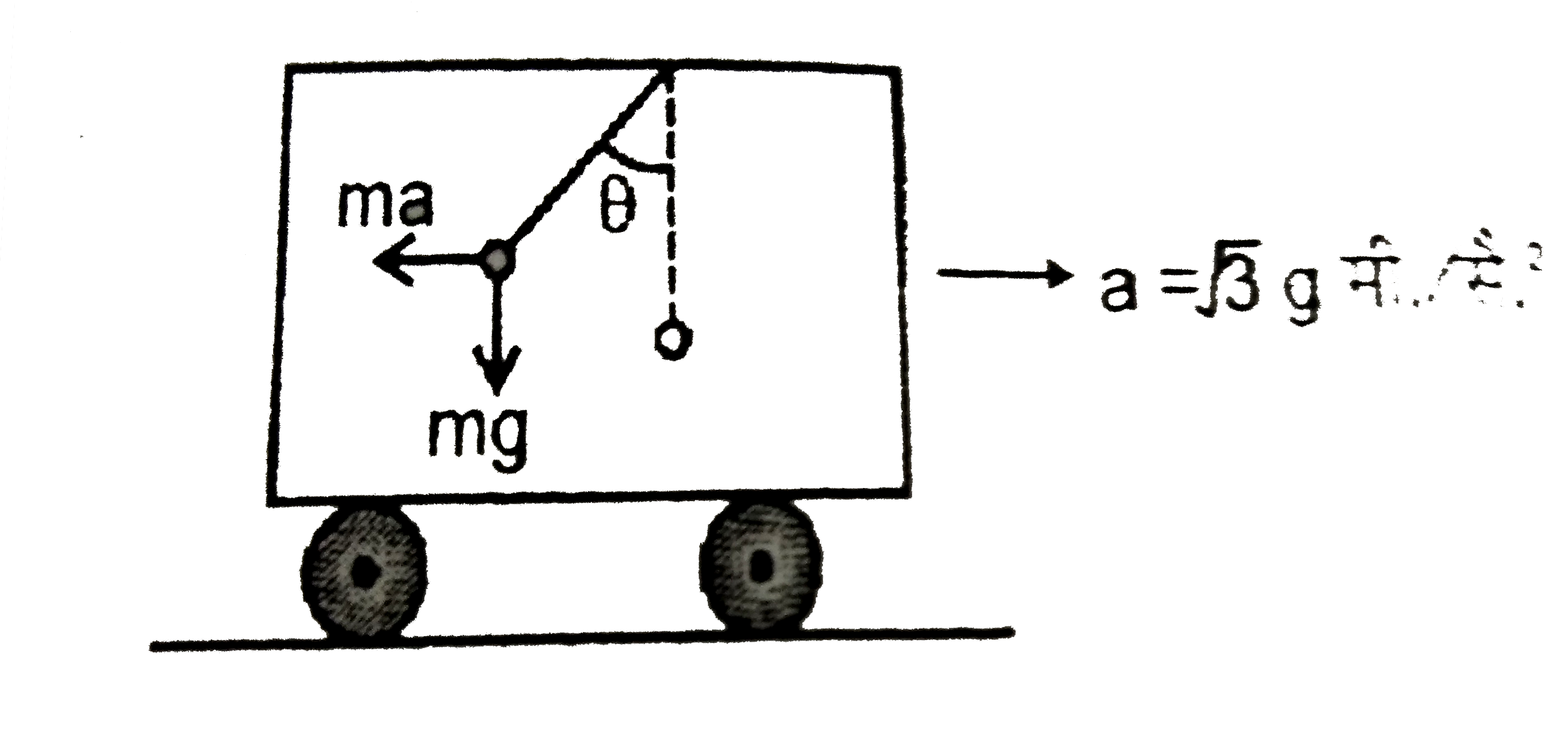
Class 11
PHYSICS
A simple pendulum 50cm long is suspended...

A simple pendulum `50cm` long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration `sqrt(3) g m//s^(-1)`. The period of small oscillations of the pendulum about its equilibrium position is `(g = pi^(2) m//s^(2))` ltbRgt

A

`1.0sec`

B

`sqrt(2)sec`

C

`1.53 sec`

D

`1.68 sec `

Text Solution

Verified by Experts

The correct Answer is:
A
With respect to the cart , equilibrium position of the pendulum is shown.
if displaced by small angle `theta` from this position, then it will execute `SHM` about his equilibrium position position, time period of whichis given by `:`


`T=2pisqrt((L)/(g_(ef f))), g_(ef f)=sqrt(g^(2)+sqrt(3g)^(2))`
`rArr g_(ef f)=2g`
`rArrT=1.0` seconds
Promotional Banner

Topper's Solved these Questions

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 76|5 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise DPP 77|8 Videos

  • DAILY PRACTICE PROBLEMS

    RESONANCE|Exercise dpp 74|7 Videos

  • CURRENT ELECTRICITY

    RESONANCE|Exercise Exercise|54 Videos

  • ELASTICITY AND VISCOCITY

    RESONANCE|Exercise Advanced Level Problems|9 Videos

Similar Questions

Explore conceptually related problems

A simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a

A simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by

A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.

A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4 m//s^(2) . Its period of oscillation is

A simple pendulum is suspended from the roof of a train. If the train is moving with an acceleration 49 cm//s^(2) . Then the angle of inclination of the string about the vertical will be

A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a_0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.

A simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration alpha , then the time period is given by T = 2pisqrt(((I)/(T))) where g is equal to

A seconds pendulum is suspended form the roof of a lift. If the lift is moving up with an acceleration 9.8 m//s^(2) , its time period is

A 60cm pendulum is fixed in an aeroplane taking off at an angle alpha=30^(@) to the horizontal with an acceleration a=4.0ms^(-2) . Determine the period of oscillation of the pendulum.

The path length of oscillation of simple pendulum of length 1 m is 16 cm. Its maximum velocity is (take, g=pi^(2)m//s^(2) )